
【题目】(1)如图,正方形![]() 中,点
中,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() ,延长
,延长![]() 到点
到点![]() ,使
,使![]() ,连结
,连结![]() ,
,![]() .求证:
.求证:![]() .
.

(2)如图,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 在边
在边![]() 上,且
上,且![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.

【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)证△ADG≌△ABE,△FAE≌△FAG,根据全等三角形的性质求出即可;
(2)过点C作CE⊥BC,垂足为点C,截取CE,使CE=BM.连接AE、EN.通过证明△ABM≌△ACE(SAS)推知全等三角形的对应边AM=AE、对应角∠BAM=∠CAE;然后由等腰直角三角形的性质和∠MAN=45°得到∠MAN=∠EAN=45°,所以△MAN≌△EAN(SAS),故全等三角形的对应边MN=EN;最后由勾股定理得到EN2=EC2+NC2即MN2=BM2+NC2.
(1)证明:在正方形![]() 中,
中,![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,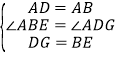 ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,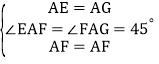 ,
,
![]() ,
,
![]() ;
;
(2)如图,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,截取
,截取![]() ,使
,使![]() .连接
.连接![]() 、
、![]() ,
,
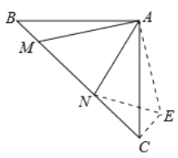
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
在![]() 和
和![]() 中,
中,
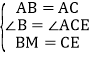 ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
于是,由![]() ,得
,得![]() ,
,
在![]() 和
和![]() 中,
中,
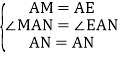 ,
,
![]() ,
,
![]() ,
,
在![]() 中,由勾股定理,得
中,由勾股定理,得![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】假设北碚万达广场地下停车场有5个出入口,每天早晨6点开始对外停车且此时车位空置率为75%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满.2019年元旦节期间,由于商场人数增多,早晨6点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨6点开始经过________小时车库恰好停满.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上每相邻两点间的距离为一个单位长度,点![]() 、
、![]() 、
、![]() 、
、![]() 对应的数分别是
对应的数分别是![]() ,且
,且![]() .
.
(1)那么![]() ,
,![]() :
:
(2)点![]() 以
以![]() 个单位/秒的速度沿着数轴的正方向运动,
个单位/秒的速度沿着数轴的正方向运动,![]() 秒后点
秒后点![]() 以
以![]() 个单位/秒的速度也沿着数轴的正方向运动,当点
个单位/秒的速度也沿着数轴的正方向运动,当点![]() 到达点
到达点![]() 处立刻返回,与点
处立刻返回,与点![]() 在数轴的某点处相遇,求这个点对应的数;
在数轴的某点处相遇,求这个点对应的数;
(3)如果![]() 、
、![]() 两点以(2)中的速度同时向数轴的负方向运动,点
两点以(2)中的速度同时向数轴的负方向运动,点![]() 从图上的位置出发也向数轴的负方向运动,且始终保持
从图上的位置出发也向数轴的负方向运动,且始终保持![]() ,当点
,当点![]() 运动到
运动到![]() 时,点
时,点![]() 对应的数是多少?
对应的数是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长.
(2)如图2,已知∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°,AC=3,AE=8,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两张宽度相等的纸条叠放在一起,重叠部分构成四边形ABCD.
(1)求证:四边形ABCD是菱形;
(2)若纸条宽3cm,∠ABC=60°,求四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市有一块长为(3a+b)米、宽为(2a+b)米的长方形地块,中间是边长为(a+b)米的正方形,规划部门计划将在中间的正方形修建一座雕像,四周的阴影部分进行绿化.
(1)绿化的面积是多少平方米?(用含字母a、b的式子表示)
(2)求出当a=10,b=12时的绿化面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB⊥BC,DC⊥BC,AB=4,CD=2,BC=8,P是BC上的一个动点,设BP=x.
(1)用关于x的代数式表示PA+PD;
(2)求出PA+PD的最小值;
(3)仿(2)的做法,构造图形,求![]() 的最小值;
的最小值;
(4)直接写出![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要900元;若购进甲种花卉40盆,乙种花卉30盆,需要960元.
(1)求购进甲、乙两种花卉每盆各需多少元?
(2)该花店购进甲,乙两种花卉共100盆,甲种花卉每盆售价20元,乙种花齐每盆售价16元,现该花店把100盆花卉全部售出,若获利超过480元,则至少购进甲种花卉多少盆?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com