
【题目】如图1,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长.
(2)如图2,已知∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°,AC=3,AE=8,求AD的长.

【答案】(1)9;(2)![]()
【解析】
试题分析:(1)连接BE,证明△ACD≌△BCE,得到AD=BE,在Rt△BAE中,AB=6![]() ,AE=3,求出BE,得到答案;
,AE=3,求出BE,得到答案;
(2)连接BE,证明△ACD∽△BCE,得到![]() =
=![]() =
=![]() ,求出BE的长,得到AD的长.
,求出BE的长,得到AD的长.
解:(1)如图1,连接BE,
∵∠ACB=∠DCE=90°,
∴∠ACB+∠ACE=∠DCE+∠ACE,即∠BCE=∠ACD,
又∵AC=BC,DC=EC,
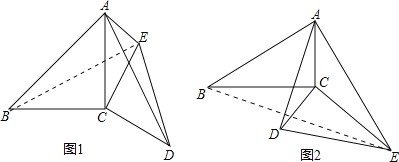
在△ACD和△BCE中,
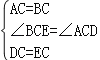 ,
,
∴△ACD≌△BCE,
∴AD=BE,
∵AC=BC=6,
∴AB=6![]() ,
,
∵∠BAC=∠CAE=45°,
∴∠BAE=90°,
在Rt△BAE中,AB=6![]() ,AE=3,
,AE=3,
∴BE=9,
∴AD=9;
(2)如图2,连接BE,
在Rt△ACB中,∠ABC=∠CED=30°,
tan30°=![]() =
=![]() ,
,
∵∠ACB=∠DCE=90°,
∴∠BCE=∠ACD,
∴△ACD∽△BCE,
∴![]() =
=![]() =
=![]() ,
,
∵∠BAC=60°,∠CAE=30°,
∴∠BAE=90°,又AB=6,AE=8,
∴BE=10,
∴AD=![]() .
.


科目:初中数学 来源: 题型:
【题目】一架云梯AB长25米,如图那样斜靠在一面墙AC上,这时云梯底端B离墙底C的距离BC为7米.
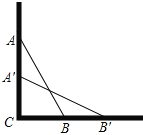
(1)这云梯的顶端距地面AC有多高?
(2)如果云梯的顶端A下滑了4米,那么它的底部B在水平方向向右滑动了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式. 比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2
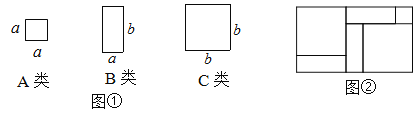

(1)取图①中的若干个(三种图形都要取到)拼成一个长方形,使它的边长分别为(2a+b)、(a+2b),不画图形,试通过计算说明需要C类卡片多少张;
(2)若取其中的若干个(三种图形都要取到)拼成一个长方形,使它的面积等于a2+5ab+4b2,画出这个长方形,并根据图形对多项式a2+5ab+4b2进行因式分解;
(3) 如图③,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案并判断,将正确关系式的序号填写在横线上______ _____(填写序号)
①.xy =![]() ②.x+y=m ③.x2-y2=m·n ④.x2+y2 =
②.x+y=m ③.x2-y2=m·n ④.x2+y2 =![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形AOBC中,OB=6,OA=4,分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上一点(不与B、C两点重合),过点F的反比例函数y=![]() (k>0)图象与AC边交于点E.
(k>0)图象与AC边交于点E.

(1)请用k的表示点E,F的坐标;
(2)若△OEF的面积为9,求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据某网站调查,2014年网民们最关注的热点话题分别有:消费、教育、环保、反腐及其他共五类.根据调查的部分相关数据,绘制的统计图表如下:
根据所给信息解答下列问题:
(1)请补全条形统计图并在图中标明相应数据;
(2)若菏泽市约有880万人口,请你估计最关注环保问题的人数约为多少万人?
(3)在这次调查中,某单位共有甲、乙、丙、丁四人最关注教育问题,现准备从这四人中随机抽取两人进行座谈,试用列表或树形图的方法求抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=BC,∠ACB=90°,点D为AC的中点.
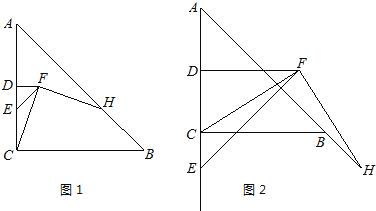
(1)如图1,E为线段DC上任意一点,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,过点F作FH⊥FC,交直线AB于点H.判断FH与FC的数量关系并加以证明;
(2)如图2,若E为线段DC的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】冬季某天我国三个城市的最高气温分别是-11℃,3℃,-3℃,它们任意两城市中最大的温差是( )
A. 6℃ B. 8℃ C. 13℃ D. 14℃
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com