
【题目】矩形ABCD的对角线交于O点,一条边的长为1,△AOB是正三角形,则这个矩形的周长为________.
【答案】2+![]() 或
或![]() .
.
【解析】
画出图形,根据矩形的对角线互相平分且相等可得AC=2OB,再根据等边三角形的三边都相等,然后求出AC=2AB,然后分①AB=1时,利用勾股定理列式求出BC,②BC=1时,利用勾股定理列式求出AB的长,再根据矩形的周长公式列式计算即可得解.
解:在矩形ABCD中,AC=2OB,
∵△AOB是正三角形,
∴OB=AB,
∴AC=2AB,
①AB=1时,AC=2,
根据勾股定理,BC=![]() ,
,
所以,矩形的周长=2(AB+BC)=2(1+![]() )=2+2
)=2+2![]() ;
;
②BC=1时,根据勾股定理,AB2+BC2=AC2,
所以,AB2+12=(2AB)2,
解得AB=![]() ,
,
所以,矩形的周长=2(AB+BC)=2(![]() +1)=
+1)=![]() +2;
+2;
综上所述,矩形的周长为2+2![]() 或
或![]() +2.
+2.
故答案为:2+2![]() 或
或![]() +2.
+2.



科目:初中数学 来源: 题型:
【题目】已知△A′B′C′是由△ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
△ABC | A(a,0) | B(3,0) | C(5,5) |
△A′B′C′ | A′(4,2) | B′(7,b) | C′(c,7) |
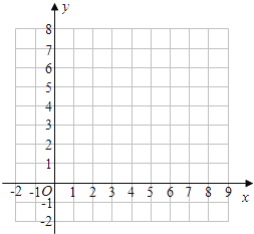
(1)观察表中各对应点坐标的变化,并填空:a=________,b=________,c=________;
(2)在平面直角坐标系中画出△ABC及平移后的△A′B′C′;
(3)直接写出△A′B′C′的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某学校学生的个性特长发展情况,在全校范围内随机抽查了部分学生参加音乐、体育、美术、书法等活动项目(每人只限一项)的情况.并将所得数据进行了统计,结果如图所示.

(1)求在这次调查中,一共抽查了多少名学生;
(2)求出扇形统计图中参加“音乐”活动项目所对扇形的圆心角的度数;
(3)若该校有2400名学生,请估计该校参加“美术”活动项目的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:① x2+y2=49;② x﹣y=2;③ x+y=9;④ 2xy+4=49;其中说法正确的是( )

A. ①②B. ①②④
C. ①②③D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月12日,安庆“筑梦号”自动驾驶公开试乘体验正式启动,让安庆成为全国率先开通自动驾驶的城市,智能、绿色出行的时代即将到来.普通燃油车从A地到B地,所需油费108元,而自动驾驶的纯电动车所需电费27元,已知每行驶l千米,普通燃油汽车所需的油费比自动的纯电动汽车所需的电费多0.54元,求自动驾驶的纯电动汽车每行驶1千米所需的电费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,BC=4,P为边AD上一动点,连接BP,把△ABP沿BP折叠,使A落在A′处,当△A′DC为等腰三角形时,AP的长为( )

A. 2B. ![]() C. 2或
C. 2或![]() D. 2或
D. 2或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雷达二维平面定位的主要原理是:测量目标的两个信息―距离和角度,目标的表示方法为![]() ,其中,m表示目标与探测器的距离;
,其中,m表示目标与探测器的距离;![]() 表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为
表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为![]() ,目标C的位置表示为
,目标C的位置表示为![]() .用这种方法表示目标B的位置,正确的是( )
.用这种方法表示目标B的位置,正确的是( )

A. (-4, 150°) B. (4, 150°) C. (-2, 150°) D. (2, 150°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“母亲节”快到了,七(1)班班委发起慰问烈士家属王大妈和李大妈的活动,决定在“母亲节”期间全班同学利用课余时间去卖鲜花筹集资金.已知同学们从花店按每枝1.4元买进鲜花,并按每枝3元卖出,设卖出鲜花x枝.
品名 | 热水壶 | 电饭煲 |
单价(单位:元/只) | 125 | 250 |
(1)每卖出一枝鲜花赚_______元,卖出鲜花x枝赚______元;
(2)若从花店购买鲜花的同时,同学们还花了50元购买包装材料,请把所筹集的资金y(元)用鲜花的销售量x(枝)的代数式表示;现在筹集的资金为750元,问需要卖出鲜花多少枝?
(3)已知两种家用小电器的单价如下表所示,现将筹集的750元全部用于购买表中家用小电器赠送两位大妈,且电饭煲至少要购买1只,请求出所有的购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com