
【题目】如图,在矩形ABCD中,AB=2,BC=4,P为边AD上一动点,连接BP,把△ABP沿BP折叠,使A落在A′处,当△A′DC为等腰三角形时,AP的长为( )

A. 2B. ![]() C. 2或
C. 2或![]() D. 2或
D. 2或![]()
【答案】C
【解析】
根据△A′DC为等腰三角形,分三种情况进行讨论:①A'D=A'C,②A'D=DC,③CA'=CD,分别求得AP的长,并判断是否符合题意.
①如图,当A′D=A′C时,过A′作EF⊥AD,交DC于E,交AB于F,则EF垂直平分CD,EF垂直平分AB

∴A'A=A'B
由折叠得,AB=A'B,∠ABP=∠A'BP
∴△ABA'是等边三角形
∴∠ABP=30°
∴AP=![]() ;
;
②如图,当A'D=DC时,A'D=2

由折叠得,A'B=AB=2
∴A'B+A'D=2+2=4
连接BD,则Rt△ABD中,BD=![]()
∴A'B+A'D<BD(不合题意)
故这种情况不存在;
③如图,当CD=CA'时,CA'=2

由折叠得,A'B=AB=2
∴A'B+A'C=2+2=4
∴点A'落在BC上的中点处
此时,∠ABP=![]() ∠ABA'=45°
∠ABA'=45°
∴AP=AB=2.
综上所述,当△A′DC为等腰三角形时,AP的长为![]() 或2.
或2.
故选C.


科目:初中数学 来源: 题型:
【题目】阅读下面资料:
小明遇到这样一个问题:如图1,对面积为a的△ABC逐次进行以下操作:分别延长AB、BC、CA至A1、B1、C1,使得A1B2AB,B1C2BC,C1A2CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1,求S1的值.

小明是这样思考和解决这个问题的:如图2,连接A1C、B1A、C1B,因为A1B2AB,B1C2BC,C1A2CA,根据等高两三角形的面积比等于底之比,所以![]()
![]() 2S△ABC2a,由此继续推理,从而解决了这个问题.
2S△ABC2a,由此继续推理,从而解决了这个问题.
(1)直接写出S1 (用含字母a的式子表示).
请参考小明同学思考问题的方法,解决下列问题:

(2)如图3,P为△ABC内一点,连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F,则把△ABC分成六个小三角形,其中四个小三角形面积已在图上标明,求△ABC的面积.
(3)如图4,若点P为△ABC的边AB上的中线CF的中点,求S△APE与S△BPF的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两张宽度相等的纸条叠放在一起,重叠部分构成四边形ABCD.
(1)求证:四边形ABCD是菱形;
(2)若纸条宽3cm,∠ABC=60°,求四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具经销商用32000元购进了一批玩具,上市后恰好全部售完;该经销商又用68000元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该经销商第二次购进这种玩具多少套?
(2)由于第二批玩具进价上涨,经销商按第一批玩具售价销售200套后,准备调整售价,发现若每套涨价1元,则会少卖5套,已知第一批玩具售价为200元.设第二批玩具销售200套后每套涨价a元,第二批卖出的玩具总利润w元,问当a取多少时,才能使售出的玩具利润w最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB⊥BC,DC⊥BC,AB=4,CD=2,BC=8,P是BC上的一个动点,设BP=x.
(1)用关于x的代数式表示PA+PD;
(2)求出PA+PD的最小值;
(3)仿(2)的做法,构造图形,求![]() 的最小值;
的最小值;
(4)直接写出![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】浠水县商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
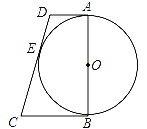
【题目】如图所示,AB是⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
(1)求证:BC为⊙O的切线;
(2)若AB=4,AD=1,求线段CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com