
【题目】阅读下面资料:
小明遇到这样一个问题:如图1,对面积为a的△ABC逐次进行以下操作:分别延长AB、BC、CA至A1、B1、C1,使得A1B2AB,B1C2BC,C1A2CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1,求S1的值.

小明是这样思考和解决这个问题的:如图2,连接A1C、B1A、C1B,因为A1B2AB,B1C2BC,C1A2CA,根据等高两三角形的面积比等于底之比,所以![]()
![]() 2S△ABC2a,由此继续推理,从而解决了这个问题.
2S△ABC2a,由此继续推理,从而解决了这个问题.
(1)直接写出S1 (用含字母a的式子表示).
请参考小明同学思考问题的方法,解决下列问题:

(2)如图3,P为△ABC内一点,连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F,则把△ABC分成六个小三角形,其中四个小三角形面积已在图上标明,求△ABC的面积.
(3)如图4,若点P为△ABC的边AB上的中线CF的中点,求S△APE与S△BPF的比值.
【答案】(1)19a;(2)315;(3)![]() .
.
【解析】
(1)首先根据题意,求得S△A1BC=2S△ABC,同理可求得S△A1B1C=2S△A1BC,依此得到S△A1B1C1=19S△ABC,则可求得面积S1的值;
(2)根据等高不等底的三角形的面积的比等于底边的比,求解,从而不难求得△ABC的面积;
(3)设S△BPF=m,S△APE=n,依题意,得S△APF=S△APC=m,S△BPC=S△BPF=m.得出![]() ,从而求解.
,从而求解.
解:(1)连接A1C,
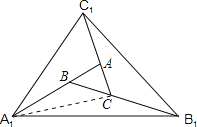
∵B1C=2BC,A1B=2AB,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
同理可得出:![]() ,
,
∴S1=6a+6a+6a+a=19a;
故答案为:19a;
(2)过点![]() 作
作![]() 于点
于点![]() ,
,
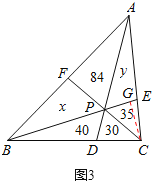
设![]() ,
,![]() ,
,
![]()
![]() ;
;![]() ,
,
![]()
 .
.
![]()
![]() ,即
,即![]() .
.
同理,![]() .
.
![]() .
.
![]() .①
.①
![]()
![]() ,
,![]() ,
,
![]()
![]() .②
.②
由①②,得![]() ,
,
![]() .
.
(3)设![]() ,
,![]() ,如图所示.
,如图所示.

依题意,得![]() ,
,![]() .
.
![]() .
.
![]()
![]() ,
,
![]()
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]()
![]() .
.
![]()
![]() .
.


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
【题目】某地电话拨号入网有两种收费方式,用户可以任选其一
A:计时制:0.05元/分,B:包月制:50元/月,此外,每一种上网时间都要收通信费0.02元/分
(1)某用户某月上网时间为x小时,请写出两种收费方式下该用户应该支付的费用(用y表示)
(2)若甲用户估计一个月上网时间为20小时,乙用户估计一个月上网时间为15小时,各选哪一种收费方式最合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某活动小组为了估计装有5个白球和若干个红球![]() 每个球除颜色外都相同
每个球除颜色外都相同![]() 的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验
的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验![]() 其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球次数为6000次.
其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球次数为6000次.
![]() 估计从袋中任意摸出一个球,恰好是红球的概率是多少?
估计从袋中任意摸出一个球,恰好是红球的概率是多少?
![]() 请你估计袋中红球接近多少个?
请你估计袋中红球接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△A′B′C′是由△ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
△ABC | A(a,0) | B(3,0) | C(5,5) |
△A′B′C′ | A′(4,2) | B′(7,b) | C′(c,7) |
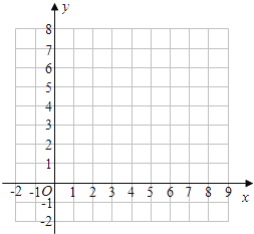
(1)观察表中各对应点坐标的变化,并填空:a=________,b=________,c=________;
(2)在平面直角坐标系中画出△ABC及平移后的△A′B′C′;
(3)直接写出△A′B′C′的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
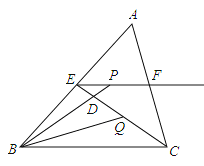
【题目】如图所示,在△ABC中,BC=12,E、F分别是AB、AC的中点,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q,当CQ=![]() CE时,EP+BP= .
CE时,EP+BP= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
氢动力汽车是一种真正实现零排放的交通工具,排放出的是纯净水,其具有无污染,零排放,储量丰富等优势,因此,氢动力汽车是传统汽车最理想的替代方案.某实验团队进行氢动力汽车实验,在一条笔直的公路上有![]() ,
,![]() 两地,小张驾驶氢动力汽车从
两地,小张驾驶氢动力汽车从![]() 地去
地去![]() 地然后立即原路返回到
地然后立即原路返回到![]() 地,小陈驾驶观察车从
地,小陈驾驶观察车从![]() 地驶向
地驶向![]() 地.如图是氢动力汽车、观察车离
地.如图是氢动力汽车、观察车离![]() 地的距离
地的距离![]() 和行驶时间
和行驶时间![]() 之间的函数图象,请根据图象回答下列问题:
之间的函数图象,请根据图象回答下列问题:

(1)![]() ,
,![]() 两地的距离是______
两地的距离是______![]() ,小陈驾驶观察车行驶的速度是______
,小陈驾驶观察车行驶的速度是______![]() ;
;
(2)当小张驾驶氢动力汽车从![]() 地原路返回
地原路返回![]() 地时,有一段时间小陈驾驶的观察车与氢动力汽车之间的距离不超过30千米,请探究此时行驶时间
地时,有一段时间小陈驾驶的观察车与氢动力汽车之间的距离不超过30千米,请探究此时行驶时间![]() 在哪一范围内?
在哪一范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD、DEFG都是正方形,连接AE、CG.

(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某学校学生的个性特长发展情况,在全校范围内随机抽查了部分学生参加音乐、体育、美术、书法等活动项目(每人只限一项)的情况.并将所得数据进行了统计,结果如图所示.

(1)求在这次调查中,一共抽查了多少名学生;
(2)求出扇形统计图中参加“音乐”活动项目所对扇形的圆心角的度数;
(3)若该校有2400名学生,请估计该校参加“美术”活动项目的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,BC=4,P为边AD上一动点,连接BP,把△ABP沿BP折叠,使A落在A′处,当△A′DC为等腰三角形时,AP的长为( )

A. 2B. ![]() C. 2或
C. 2或![]() D. 2或
D. 2或![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com