
【题目】如图,四边形ABCD、DEFG都是正方形,连接AE、CG.

(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想.
【答案】(1)见解析;(2)AE⊥CG
【解析】
试题分析:可以把结论涉及的线段放到△ADE和△CDG中,考虑证明全等的条件,又有两个正方形,∴AD=CD,DE=DG,它们的夹角都是∠ADG加上直角,故夹角相等,可以证明全等;再利用互余关系可以证明AE⊥CG.
(1)如图,
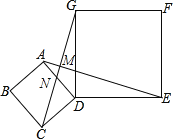
∵AD=CD,DE=DG,∠ADC=∠GDE=90°,
又∵∠CDG=90°+∠ADG=∠ADE,
∴△ADE≌△CDG(SAS).
∴AE=CG.
(2)如图,设AE与CG交点为M,AD与CG交点为N.
∵△ADE≌△CDG,
∴∠DAE=∠DCG.
又∵∠ANM=∠CND,
∴△AMN∽△CDN.
∴∠AMN=∠ADC=90°.
∴AE⊥CG.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】“五一”期间,小明和父母一起开车到距家![]() 的景点旅游,出发前,汽车油箱内储油
的景点旅游,出发前,汽车油箱内储油![]() ,当行驶
,当行驶![]() 时,发现油箱余油量为
时,发现油箱余油量为![]() (假设行驶过程中汽车的耗油量是均匀的).
(假设行驶过程中汽车的耗油量是均匀的).
(1)这个变化过程中哪个是自变量?哪个是因变量?
(2)求该车平均每千米的耗油量,并写出行驶路程![]() 与剩余油量
与剩余油量![]() 的关系式;
的关系式;
(3)当![]() 时,求剩余油量
时,求剩余油量![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数![]() 都可以进行这样的分解:
都可以进行这样的分解:![]() (
(![]() 是正整数,且
是正整数,且![]() ),在
),在![]() 的所有这种分解中,如果
的所有这种分解中,如果![]() 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称![]() 是
是![]() 的最佳分解,产规定:
的最佳分解,产规定:![]() ,例如:12可以分解成
,例如:12可以分解成![]() ,
,![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() 是12的最佳分解,所以
是12的最佳分解,所以![]() .
.
(1)求![]() ;
;
(2)若正整数![]() 是4的倍数,我们称正整数
是4的倍数,我们称正整数![]() 为“四季数”,如果一个两位正整数
为“四季数”,如果一个两位正整数![]() ,
,![]() (
(![]() ,
,![]() 为自然数),交换个位上的数字与十位上的数字得到的新两位正整数减去原来的两位正整数所得的差为“四季数”,那么我们称这个数
为自然数),交换个位上的数字与十位上的数字得到的新两位正整数减去原来的两位正整数所得的差为“四季数”,那么我们称这个数![]() 为“有缘数”,求所有“有缘数”中
为“有缘数”,求所有“有缘数”中![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面资料:
小明遇到这样一个问题:如图1,对面积为a的△ABC逐次进行以下操作:分别延长AB、BC、CA至A1、B1、C1,使得A1B2AB,B1C2BC,C1A2CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1,求S1的值.

小明是这样思考和解决这个问题的:如图2,连接A1C、B1A、C1B,因为A1B2AB,B1C2BC,C1A2CA,根据等高两三角形的面积比等于底之比,所以![]()
![]() 2S△ABC2a,由此继续推理,从而解决了这个问题.
2S△ABC2a,由此继续推理,从而解决了这个问题.
(1)直接写出S1 (用含字母a的式子表示).
请参考小明同学思考问题的方法,解决下列问题:

(2)如图3,P为△ABC内一点,连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F,则把△ABC分成六个小三角形,其中四个小三角形面积已在图上标明,求△ABC的面积.
(3)如图4,若点P为△ABC的边AB上的中线CF的中点,求S△APE与S△BPF的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.

(1)如图1,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,且
上的点,且![]() ,求证:
,求证:![]() 为等腰直角三角形.
为等腰直角三角形.
(2)如图2,若![]() 、
、![]() 分别为
分别为![]() ,
,![]() 延长线上的点,仍有
延长线上的点,仍有![]() ,其他条件不变,那么,
,其他条件不变,那么,![]() 是否仍为等腰直角三角形?证明你的结论.
是否仍为等腰直角三角形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上每相邻两点间的距离为一个单位长度,点![]() 、
、![]() 、
、![]() 、
、![]() 对应的数分别是
对应的数分别是![]() ,且
,且![]() .
.
(1)那么![]() ,
,![]() :
:
(2)点![]() 以
以![]() 个单位/秒的速度沿着数轴的正方向运动,
个单位/秒的速度沿着数轴的正方向运动,![]() 秒后点
秒后点![]() 以
以![]() 个单位/秒的速度也沿着数轴的正方向运动,当点
个单位/秒的速度也沿着数轴的正方向运动,当点![]() 到达点
到达点![]() 处立刻返回,与点
处立刻返回,与点![]() 在数轴的某点处相遇,求这个点对应的数;
在数轴的某点处相遇,求这个点对应的数;
(3)如果![]() 、
、![]() 两点以(2)中的速度同时向数轴的负方向运动,点
两点以(2)中的速度同时向数轴的负方向运动,点![]() 从图上的位置出发也向数轴的负方向运动,且始终保持
从图上的位置出发也向数轴的负方向运动,且始终保持![]() ,当点
,当点![]() 运动到
运动到![]() 时,点
时,点![]() 对应的数是多少?
对应的数是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(生活常识)
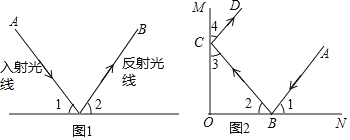
射到平面镜上的光线(入射光线)和变向后的光线(反射光线)与平面镜所夹的角相等。如图 1,MN 是平面镜,若入射光线 AO 与水平镜面夹角为∠1,反射光线 OB 与水平镜面夹角为∠2,则∠1=∠2 .
(现象解释)
如图 2,有两块平面镜 OM,ON,且 OM⊥ON,入射光线 AB 经过两次反射,得到反射光线 CD.求证 AB∥CD.
(尝试探究)
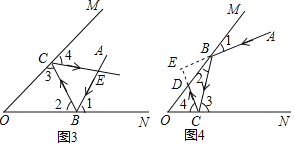
如图 3,有两块平面镜 OM,ON,且∠MON =55 ,入射光线 AB 经过两次反射,得到反射光线 CD,光线 AB 与 CD 相交于点 E,求∠BEC 的大小.
(深入思考)
如图 4,有两块平面镜 OM,ON,且∠MON α ,入射光线 AB 经过两次反射,得到反射光线 CD,光线 AB 与 CD 所在的直线相交于点 E,∠BED=β , α 与 β 之间满足的等量关系是 .(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两张宽度相等的纸条叠放在一起,重叠部分构成四边形ABCD.
(1)求证:四边形ABCD是菱形;
(2)若纸条宽3cm,∠ABC=60°,求四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】浠水县商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com