
【题目】已知:在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.

(1)如图1,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,且
上的点,且![]() ,求证:
,求证:![]() 为等腰直角三角形.
为等腰直角三角形.
(2)如图2,若![]() 、
、![]() 分别为
分别为![]() ,
,![]() 延长线上的点,仍有
延长线上的点,仍有![]() ,其他条件不变,那么,
,其他条件不变,那么,![]() 是否仍为等腰直角三角形?证明你的结论.
是否仍为等腰直角三角形?证明你的结论.
【答案】(1)见解析;(2)见解析.
【解析】
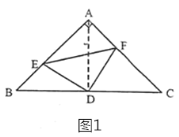
(1)先连接AD,构造全等三角形:△BED和△AFD.AD是等腰直角三角形ABC底边上的中线,所以有∠CAD=∠BAD=45°,AD=BD=CD,而∠B=∠C=45°,所以∠B=∠DAF,再加上BE=AF,AD=BD,可证出:![]() ,从而得出DE=DF,∠BDE=∠ADF,从而得出∠EDF=90°,即△DEF是等腰直角三角形;
,从而得出DE=DF,∠BDE=∠ADF,从而得出∠EDF=90°,即△DEF是等腰直角三角形;
(2)还是证明:![]() ,主要证∠DAF=∠DBE(∠DBE=180°-45°=135°,∠DAF=90°+45°=135°),再结合两组对边对应相等,所以两个三角形全等.
,主要证∠DAF=∠DBE(∠DBE=180°-45°=135°,∠DAF=90°+45°=135°),再结合两组对边对应相等,所以两个三角形全等.
(1)证明:连结![]() ,如图1所示,
,如图1所示,
∵![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() .
.
∴![]() ,
,![]() ,
,
∴![]()
![]() .
.
∴![]() 为等腰直角三角形;
为等腰直角三角形;
(2)若![]() 、
、![]() 分别是
分别是![]() 、
、![]() 延长线上的点,连结
延长线上的点,连结![]() ,如图2所示,
,如图2所示,

∵![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
![]() .
.
∴![]() 仍为等腰直角三角形.
仍为等腰直角三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
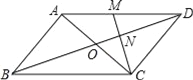
【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《山西省新能源汽车产业2018年行动计划》指出,2018年全省新能源汽车产能将达到30万辆,按照“十三五”规划,到2020年,全省新能源汽车产能将达到41万辆,若设这两年全省新能源汽车产能的平均增长率为![]() ,则根据题意可列出方程是()
,则根据题意可列出方程是()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
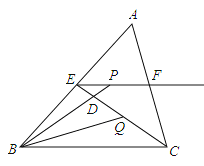
【题目】如图所示,在△ABC中,BC=12,E、F分别是AB、AC的中点,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q,当CQ=![]() CE时,EP+BP= .
CE时,EP+BP= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO等于( )

A. 1︰1︰1
B. 1︰2︰3
C. 2︰3︰4
D. 3︰4︰5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD、DEFG都是正方形,连接AE、CG.

(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
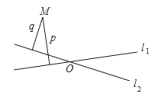
【题目】如图,直线![]() 与
与![]() 相交于点
相交于点![]() ,对于平面内任意一点
,对于平面内任意一点![]() ,点
,点![]() 直线
直线![]() ,
,![]() 的距离分别为
的距离分别为![]() ,
,![]() ,则称有序实数对
,则称有序实数对![]() 是点
是点![]() 的“距离坐标”,根据上述定义,“距离坐标”是
的“距离坐标”,根据上述定义,“距离坐标”是![]() 的点的个数是( )
的点的个数是( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
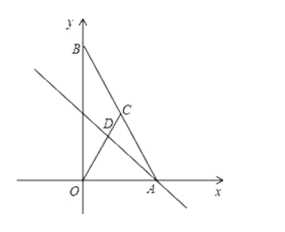
【题目】如图,在平面直角坐标系中,![]() 为直线
为直线![]() 与直线
与直线![]() 的交点,点
的交点,点![]() 在线段
在线段![]() 上,
上,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)若![]() 为线段
为线段![]() 上一动点(不与
上一动点(不与![]() 重合),
重合),![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,请求出
,请求出![]() 与
与![]() 的函数关系式;
的函数关系式;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.
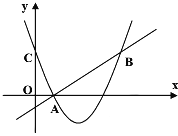
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b≥(x-2)2+m的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com