【题目】《山西省新能源汽车产业2018年行动计划》指出，2018年全省新能源汽车产能将达到30万辆，按照“十三五”规划，到2020年，全省新能源汽车产能将达到41万辆，若设这两年全省新能源汽车产能的平均增长率为
，则根据题意可列出方程是（）
A. 
B. 
C. 
D. 
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
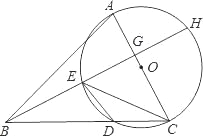
【题目】已知：在△ABC中，以AC边为直径的⊙O交BC于点D，在劣弧
上取一点E使∠EBC=∠DEC，延长BE依次交AC于点G，交⊙O于H．
（1）求证：AC⊥BH；
（2）若∠ABC=45°，⊙O的直径等于10，BD=8，求CE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平面直角坐标系中，平行四边形ABCD的中心E的坐标为(2，0)，若点A的坐标为(-2，1)，则点C的坐标为( )
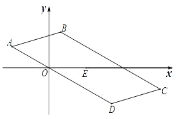
A. (4，-1)B. (6，-1)C. (8，-1)D. (6，-2)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，长方形ABCD中，AB=4，AD=2，点Q与点P同时从点A出发，点Q以每秒1个单位的速度沿A→D→C→B的方向运动，点P以每秒3个单位的速度沿A→B→C→D的方向运动，当P、Q两点相遇时，它们同时停止运动。设Q点运动的时间为
(秒)，在整个运动过程中,求解下面问题:
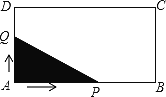
（1）当P、Q相遇时，求出的值(列方程解决问题)；
（2）当△APQ的面积为
时，此时t的值是_________；
（3）当△APQ为直角三角形时,直接写出相应的的值或取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们知道，任意一个正整数
都可以进行这样的分解：
（
是正整数，且
），在的所有这种分解中，如果两因数之差的绝对值最小，我们就称
是的最佳分解，产规定：
，例如：12可以分解成
，
，
，因为
，所以是12的最佳分解，所以
.
（1）求
；
（2）若正整数
是4的倍数，我们称正整数为“四季数”，如果一个两位正整数
，
（
，
为自然数），交换个位上的数字与十位上的数字得到的新两位正整数减去原来的两位正整数所得的差为“四季数”，那么我们称这个数为“有缘数”，求所有“有缘数”中
的最小值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】平行四边形ABCD中，对角线AC、BD相交于点O，BD=2AD，E、F、G分别是OC、OD，AB的中点．下列结论：①EG=EF；②△EFG≌△GBE；③FB平分∠EFG；④EA平分∠GEF；⑤四边形BEFG是菱形．其中正确的是______．
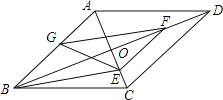
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：在
中，
，
，点
为
的中点.
（1）如图1，
、
分别是
、
上的点，且
，求证：
为等腰直角三角形.
（2）如图2，若、分别为，
延长线上的点，仍有，其他条件不变，那么，是否仍为等腰直角三角形？证明你的结论.
查看答案和解析>>
科目：初中数学 来源： 题型：
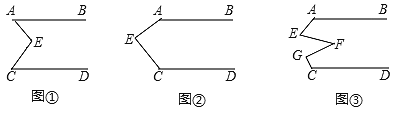
【题目】（感知）如图①，AB∥CD，点E在直线AB与CD之间，连结AE、BE，试说明∠BAE+∠DCE=∠AEC；
（探究）当点E在如图②的位置时，其他条件不变，试说明∠AEC+∠BAE+∠DCE=360°；
（应用）点E、F、G在直线AB与CD之间，连结AE、EF、FG和CG，其他条件不变，如图③，若∠EFG=36°，则∠BAE+∠AEF+∠FGC+∠DCG=______°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
