
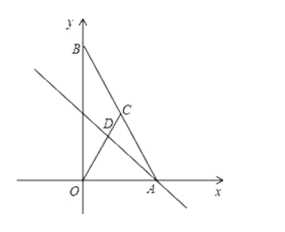
【题目】如图,在平面直角坐标系中,![]() 为直线
为直线![]() 与直线
与直线![]() 的交点,点
的交点,点![]() 在线段
在线段![]() 上,
上,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)若![]() 为线段
为线段![]() 上一动点(不与
上一动点(不与![]() 重合),
重合),![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,请求出
,请求出![]() 与
与![]() 的函数关系式;
的函数关系式;
科目:初中数学 来源: 题型:
【题目】已知:在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.

(1)如图1,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,且
上的点,且![]() ,求证:
,求证:![]() 为等腰直角三角形.
为等腰直角三角形.
(2)如图2,若![]() 、
、![]() 分别为
分别为![]() ,
,![]() 延长线上的点,仍有
延长线上的点,仍有![]() ,其他条件不变,那么,
,其他条件不变,那么,![]() 是否仍为等腰直角三角形?证明你的结论.
是否仍为等腰直角三角形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(生活常识)
射到平面镜上的光线(入射光线)和变向后的光线(反射光线)与平面镜所夹的角相等。如图 1,MN 是平面镜,若入射光线 AO 与水平镜面夹角为∠1,反射光线 OB 与水平镜面夹角为∠2,则∠1=∠2 .
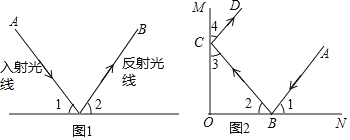
(现象解释)
如图 2,有两块平面镜 OM,ON,且 OM⊥ON,入射光线 AB 经过两次反射,得到反射光线 CD.求证 AB∥CD.
(尝试探究)
如图 3,有两块平面镜 OM,ON,且∠MON =55 ,入射光线 AB 经过两次反射,得到反射光线 CD,光线 AB 与 CD 相交于点 E,求∠BEC 的大小.
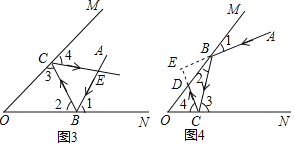
(深入思考)
如图 4,有两块平面镜 OM,ON,且∠MON α ,入射光线 AB 经过两次反射,得到反射光线 CD,光线 AB 与 CD 所在的直线相交于点 E,∠BED=β , α 与 β 之间满足的等量关系是 .(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
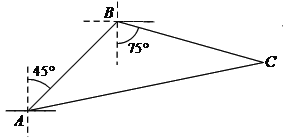
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两张宽度相等的纸条叠放在一起,重叠部分构成四边形ABCD.
(1)求证:四边形ABCD是菱形;
(2)若纸条宽3cm,∠ABC=60°,求四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(感知)如图①,AB∥CD,点E在直线AB与CD之间,连结AE、BE,试说明∠BAE+∠DCE=∠AEC;
(探究)当点E在如图②的位置时,其他条件不变,试说明∠AEC+∠BAE+∠DCE=360°;
(应用)点E、F、G在直线AB与CD之间,连结AE、EF、FG和CG,其他条件不变,如图③,若∠EFG=36°,则∠BAE+∠AEF+∠FGC+∠DCG=______°.
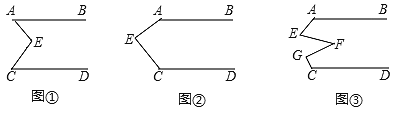
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具经销商用32000元购进了一批玩具,上市后恰好全部售完;该经销商又用68000元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该经销商第二次购进这种玩具多少套?
(2)由于第二批玩具进价上涨,经销商按第一批玩具售价销售200套后,准备调整售价,发现若每套涨价1元,则会少卖5套,已知第一批玩具售价为200元.设第二批玩具销售200套后每套涨价a元,第二批卖出的玩具总利润w元,问当a取多少时,才能使售出的玩具利润w最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ADC=130°,∠ABC=∠ADC,BF、DE分别平分∠ABC与∠ADC,交对边于F、E,且∠ABF=∠AED,过E作EH⊥AD交AD于H。
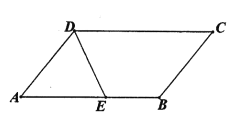
(1)在图中作出线段BF和EH(不要求尺规作图);
(2)求∠AEH的大小。
小亮同学根据条件进行推理计算,得出结论,请你在括号内注明理由。
证明:∵BF、DE分别平分∠ABC与∠ADC,(已知)
∴∠ABF=![]() ∠ABC,∠CDE=
∠ABC,∠CDE=![]() ∠ADC。( )
∠ADC。( )
∵∠ABC=∠ADC,(已知)
∴∠ABF=∠CDE。(等式的性质)
∵∠ABF=∠AED,(已知)
∴∠CDE=∠AED。( )
∴AB∥CD。( )
∵∠ADC=130°(已知)
∴∠A=180°-∠ADC=50°(两直线平行,同旁内角互补)
∵EH⊥AD于H(已知)
∴∠EHA=90°(垂直的定义)
∴在Rt△AEH中,∠AEH=90°-∠A( )=40°。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com