
【题目】己知关于x的一元二次方程x2+(2k+3)x+k2=0有两个不相等的实数根x1,x2.
(1)求k的取值范围;
(2)若![]() =﹣1,求k的值.
=﹣1,求k的值.
【答案】(1)k>﹣![]() ;(2)k=3.
;(2)k=3.
【解析】(1)根据方程的系数结合根的判别式△>0,即可得出关于k的一元一次方程,解之即可得出k的取值范围;
(2)根据根与系数的关系可得出x1+x2=﹣2k﹣3、x1x2=k2,结合![]() =﹣1即可得出关于k的分式方程,解之经检验即可得出结论.
=﹣1即可得出关于k的分式方程,解之经检验即可得出结论.
(1)∵关于x的一元二次方程x2+(2k+3)x+k2=0有两个不相等的实数根,
∴△=(2k+3)2﹣4k2>0,
解得:k>﹣![]() ;
;
(2)∵x1、x2是方程x2+(2k+3)x+k2=0的实数根,
∴x1+x2=﹣2k﹣3,x1x2=k2,
∴![]() =﹣1,
=﹣1,
解得:k1=3,k2=﹣1,
经检验,k1=3,k2=﹣1都是原分式方程的根,
又∵k>﹣![]() ,
,
∴k=3.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
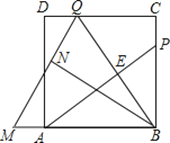
【题目】如图,P为正方形ABCD的边BC上一动点(P与B.C不重合),点Q在CD边上,且BP=CQ,连接AP、BQ交于点E,将△BQC沿BQ所在直线对折得到△BQN,延长QN交BA的延长线于点M.
(1)求证:AP⊥BQ;
(2)若AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对一张矩形纸片ABCD进行折叠,具体操作如下:
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再一次折叠,使点A落在MN上的点A′处,并使折痕经过点B,得到折痕BE,同时,得到线段BA′,EA′,展开,如图1;
第三步:再沿EA′所在的直线折叠,点B落在AD上的点B′处,得到折痕EF,同时得到线段B′F,展开,如图2.
求证:(1)∠ABE=30°;
(2)四边形BFB′E为菱形.
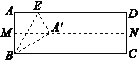

图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
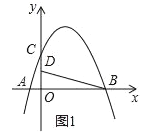
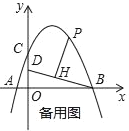
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+4交x轴于点A(﹣2,0)和B(B在A右侧),交y轴于点C,直线y=![]() 经过点B,交y轴于点D,且D为OC中点.
经过点B,交y轴于点D,且D为OC中点.
(1)求抛物线的解析式;
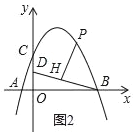
(2)若P是第一象限抛物线上的一点,过P点作PH⊥BD于H,设P点的横坐标是t,线段PH的长度是d,求d与t的函数关系式;
(3)在(2)的条件下,当d=![]() 时,将射线PH绕着点P顺时针方向旋转45°交抛物线于点Q,求点Q的坐标.
时,将射线PH绕着点P顺时针方向旋转45°交抛物线于点Q,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,点P在AD上,AB=![]() ,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB,BC于点E,F,连接EF(如图).
,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB,BC于点E,F,连接EF(如图).

(1)当点E与点B重合时,点F恰好与点C重合(如图),则PC的长为 ;
(2)将直角尺从如图中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中,从开始到停止,线段EF的中点所经过的路径(线段)长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)①如图1,已知![]() ,
,![]() ,可得
,可得![]() __________.
__________.

②如图2,在①的条件下,如果![]() 平分
平分![]() ,则
,则![]() __________.
__________.

③如图3,在①、②的条件下,如果![]() ,则
,则![]() __________.
__________.

(2)尝试解决下面问题:已知如图4,![]() ,
,![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() ,求
,求![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
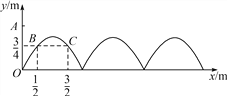
【题目】如图,需在一面墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用y=ax2+bx(a≠0)表示.已知抛物线上B,C两点到地面的距离均为![]() m,到墙边OA的距离分别为
m,到墙边OA的距离分别为![]() m,
m,![]() m.
m.
(1)求该拋物线的函数关系式,并求图案最高点到地面的距离;
(2)若该墙的长度为10 m,则最多可以连续绘制几个这样的拋物线型图案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】单位为了解3500名党员职工每月党费上交情况,从中随机抽取50名党员职工,根据每月每名党员职工的党费情况给制如图所示的条形统计图.
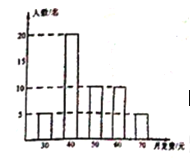
(1)求50名党职工每月觉费的平均数;
(2)直接写出这50名党员职工每月党费的众数与中位数;
(3)根据这50名党员职工每月党费的平均数,请你估计该单位3500名党员职工每月约上交党费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以线段
,以线段![]() 为边向外作等边
为边向外作等边![]() ,点
,点![]() 是线段
是线段![]() 的中点,连结
的中点,连结![]() 并延长交线段
并延长交线段![]() 于点
于点![]() .
.
(1)求证:四边形![]() 为平行四边形;
为平行四边形;
(2)求平行四边形![]() 的面积;
的面积;
(3)如图,分别作射线![]() ,
,![]() ,如图中
,如图中![]() 的两个顶点
的两个顶点![]() ,
,![]() 分别在射线
分别在射线![]() ,
,![]() 上滑动,在这个变化的过程中,求出线段
上滑动,在这个变化的过程中,求出线段![]() 的最大长度.
的最大长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com