
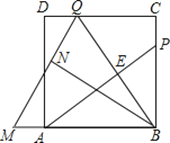
【题目】如图,P为正方形ABCD的边BC上一动点(P与B.C不重合),点Q在CD边上,且BP=CQ,连接AP、BQ交于点E,将△BQC沿BQ所在直线对折得到△BQN,延长QN交BA的延长线于点M.
(1)求证:AP⊥BQ;
(2)若AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长。
【答案】(1)证明见解析;(2)MQ=![]() ;(3)AM=
;(3)AM=![]() .
.
【解析】
试题(1)证明△ABP≌△BCQ,则∠BAP=∠CBQ,从而证明∠CBQ+∠APB=90°,进而得证;
(2)设MQ=MB=x,则MN=x﹣2.在直角△MBN中,利用勾股定理即可列方程求解;
(3)设AM=y,BN=BC=m+n,在直角△BNM中,MB=y+m+n,MN=MQ﹣QN=(y+m+n)﹣m=y+n,利用勾股定理即可求解.
试题解析:(1)证明:∵四边形ABCD是正方形,∴∠ABC=∠C=90°,AB=BC,在△ABP和△BCQ中,∵AB=BC,∠ABC=∠C,BP=CQ,∴△ABP≌△BCQ,∴∠BAP=∠CBQ.
∵∠BAP+∠APB=90°,∴∠CBQ+∠APB=90°,∴∠BEP=90°,∴AP⊥BQ;
(2)解:∵正方形ABCD中,AB=3,BP=2CP,∴BP=2,由(1)可得NQ=CQ=BP=2,NB=3.
又∵∠NQB=∠CQB=∠ABQ,∴MQ=MB.
设MQ=MB=x,则MN=x﹣2.
在直角△MBN中,![]() ,即
,即![]() ,解得:x=
,解得:x=![]() ,即MQ=
,即MQ=![]() ;
;
(3)∵BP=m,CP=n,由(1)(2)得MQ=BM,CQ=QN=BP=m,设AM=y,BN=BC=m+n,在直角△BNM中,MB=y+m+n,MN=MQ﹣QN=(y+m+n)﹣m=y+n,![]() ,即
,即![]() ,则y=
,则y=![]() ,AM=
,AM=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
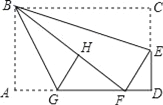
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
①∠EBG=45°;②△DEF∽△ABG;③S△ABG=![]() S△FGH;④AG+DF=FG.
S△FGH;④AG+DF=FG.
其中正确的是__.(把所有正确结论的序号都选上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由一些正整数组成的数表如下(表中下一行中数的个数是上一行中数的个数的2倍):

若规定坐标号(m,n)表示第m行从左向右第n个数,则(7,4)所表示的数是_____;(5,8)与(8,5)表示的两数之积是_______;数2012对应的坐标号是_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 O 是等边△ABC 内一点,∠AOB=105°,∠BOC 等于α,将△BOC 绕点 C 按 顺时针方向旋转 60°得△ADC,连接 OD.
(1)求证:△COD 是等边三角形.
(2)求∠OAD 的度数.
(3)探究:当α为多少度时,△AOD 是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列命题:
①在直角三角形ABC中,已知两边长为3和4,则第三边长为5;
②三角形的三边a、b、c满足a2+c2=b2,则∠C=90°;
③△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;
④△ABC中,若 a:b:c=1:2:![]() ,则这个三角形是直角三角形.
,则这个三角形是直角三角形.
其中,正确命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
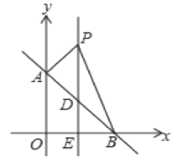
【题目】如图,平面直角坐标系中,直线AB:y=x+b交y轴于点A(0,4),交x轴于点B.
(1)求点B的坐标;
(2)直线l垂直平分OB交AB于点D,交x轴于点E,点P是直线l上一动点,且在点D的上方,设点P的纵坐标为n.
①用含n的代数式表示△ABP的面积;
②当S△ABP=8时,求点P的坐标;
(3)在(2)中②的条件下,以PB为斜边作等腰直角△PBC,求点C的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
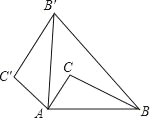
【题目】如图,将△ABC绕点A逆时针旋转80°后得到△A′B′C′(点B的对应点是点B′,点C的对应点是点C′,连接BB′,若∠B′BC=20°,则∠BB′C′的大小是( )
A. 82° B. 80° C. 78° D. 76°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com