
【题目】由一些正整数组成的数表如下(表中下一行中数的个数是上一行中数的个数的2倍):

若规定坐标号(m,n)表示第m行从左向右第n个数,则(7,4)所表示的数是_____;(5,8)与(8,5)表示的两数之积是_______;数2012对应的坐标号是_________
【答案】134, 12144, (10,495).
【解析】
根据下一行中数的个数是上一行中数的个数的2倍表示出前n行偶数的个数的表达式为2m-1,然后求出第6行的最后一个偶数,再计算之后的4个偶数即可求出(7,4);分别求出第4行第7行最后的一个偶数,然后求出(5,8)与(8,5)表示的数,再相乘即可;求出数2012是第1006个偶数,根据表达式得1006=29-1+495,先求出第511个数是第9行的最后一个数,再求解即可.
解:设前m行偶数的个数为S,
则S=1+2+22+23+…+2m-1,
两边都乘以2得,2S=2+22+23+…+2m,
所以,S=2m-1,
当m=6时,S=26-1=64-1=63,
所以,(7,4)所表示的数是第63+4=67个偶数,为134;
当n=4时,24-1=15,
所以,(5,8)表示的数是第15+8=23个偶数,为46,
当n=7时,27-1=127,
所以,(8,5)表示的数是第127+5=132个偶数,为264,
46×264=12144;
∵数2012是第1006个偶数,
n=9时,29-1=511,1006-511=495
∴数2012是第10行的第495个数,可以表示为(10,495).
故答案为:20,12144,(10,495).


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
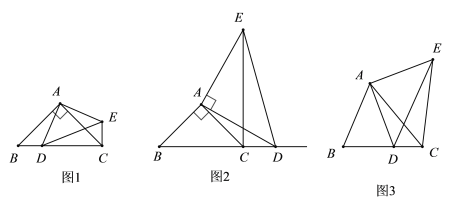
【题目】如图,在△ABC中,∠ABC为锐角,点D为直线BC上一动点,以AD为直角边且在AD的右侧作等腰直角三角形ADE,∠DAE=90°,AD=AE.
(1)如果AB=AC,∠BAC=90°.①当点D在线段BC上时,如图1,线段CE、BD的位置关系为___________,数量关系为___________
②当点D在线段BC的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
(2)如图3,如果AB≠AC,∠BAC≠90°,点D在线段BC上运动。探究:当∠ACB多少度时,CE⊥BC?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
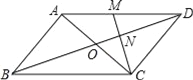
【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有若干个相同的红球,为了估计袋中红球的数量,某学习小组做了摸球实验,他们将30个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复![]() 下表是几次活动汇总后统计的数据:
下表是几次活动汇总后统计的数据:
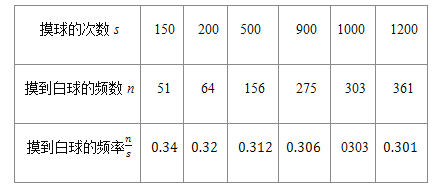
![]() 请估计:当次数s很大时,摸到白球的频率将会接近______ ;假如你去摸一次,你摸到红球的概率是______
请估计:当次数s很大时,摸到白球的频率将会接近______ ;假如你去摸一次,你摸到红球的概率是______ ![]() 精确到
精确到![]() .
.
![]() 试估算口袋中红球有多少只?
试估算口袋中红球有多少只?
![]() 解决了上面的问题后请你从统计与概率方面谈一条启示.
解决了上面的问题后请你从统计与概率方面谈一条启示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
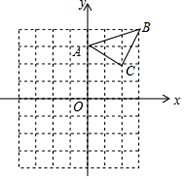
(1)△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;(画出图形)
(3)△A2B2C2的面积是 平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织1000名学生参加“展示我美丽祖国”庆国庆的自拍照片的评比活动.随机机取一些学生在评比中的成绩制成的统计图表如下:


根据以上图表提供的信息,解答下列问题:
(1)写出表中a、b的数值:a ,b ;
(2)补全频数分布表和频数分布直方图;
(3)如果评比成绩在95分以上(含95 分)的可以获得一等奖,试估计该校参加此次活动获得一等 奖的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
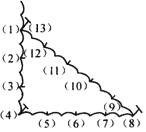
【题目】古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( )
A. 直角三角形两个锐角互补
B. 三角形内角和等于180°
C. 如果三角形两条边长的平方和等于第三边长的平方
D. 如果三角形两条边长的平方和等于第三边长的平方,那么这个三角形是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
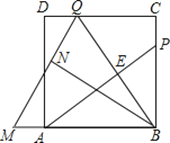
【题目】如图,P为正方形ABCD的边BC上一动点(P与B.C不重合),点Q在CD边上,且BP=CQ,连接AP、BQ交于点E,将△BQC沿BQ所在直线对折得到△BQN,延长QN交BA的延长线于点M.
(1)求证:AP⊥BQ;
(2)若AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对一张矩形纸片ABCD进行折叠,具体操作如下:
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再一次折叠,使点A落在MN上的点A′处,并使折痕经过点B,得到折痕BE,同时,得到线段BA′,EA′,展开,如图1;
第三步:再沿EA′所在的直线折叠,点B落在AD上的点B′处,得到折痕EF,同时得到线段B′F,展开,如图2.
求证:(1)∠ABE=30°;
(2)四边形BFB′E为菱形.
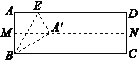

图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com