
ЁОЬтФПЁПФГТУааЩчЭЦГівЛЬѕГЩБОМлЮЛ500дЊ/ШЫЕФЪЁФкТУгЮЯпТЗЃЌгЮПЭШЫЪ§yЃЈШЫ/дТЃЉгыТУгЮБЈМлxЃЈдЊ/ШЫЃЉжЎМфЕФЙиЯЕЮЊy=Љx+1300ЃЌвбжЊЃКТУгЮжїЙмВПУХЙцЖЈИУТУгЮЯпТЗБЈМлдк800дЊ/ШЫЁЋ1200дЊ/ШЫжЎМфЃЎ
ЃЈ1ЃЉвЊНЋИУТУгЮЯпТЗУПдТгЮПЭШЫЪ§ПижЦдк200ШЫвдФкЃЌЧѓИУТУгЮЯпТЗБЈМлЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЧѓОгЊетЬѕТУгЮЯпТЗУПдТЫљашвЊЕФзюЕЭГЩБОЃЛ
ЃЈ3ЃЉЕЕетЬѕТУгЮЯпТЗЕФТУгЮБЈМлЮЊЖрЩйЪБЃЌПЩЛёЕУзюДѓРћШѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ЁОД№АИЁПЃЈ1ЃЉШЁжЕЗЖЮЇЮЊ1100дЊ/ШЫЁЋ1200дЊ/ШЫжЎМфЃЛЃЈ2ЃЉ50000ЃЛЃЈ3ЃЉx=900ЪБЃЌwзюДѓ=160000
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЬтвтСаВЛЕШЪНЧѓНтПЩЃЛ
ЃЈ2ЃЉИљОнБЈМлМѕШЅГЩБОПЩЕУЕНКЏЪ§ЕФНтЮіЪНЃЌИљОнвЛДЮКЏЪ§ЕФЭМЯёЧѓНтМДПЩЃЛ
ЃЈ3ЃЉИљОнРћШѓЕШгкШЫДЮГЫвдМлИёМДПЩЕУЕНКЏЪ§ЕФНтЮіЪНЃЌШЛКѓИљОнЖўДЮКЏЪ§ЕФзюжЕЧѓНтМДПЩ.
ЪдЬтНтЮіЃКЃЈ1ЃЉЁпгЩЬтвтЕУ![]() ЪБЃЌМД
ЪБЃЌМД![]() ЃЌ
ЃЌ
ЁрНтЕУ![]()
МДвЊНЋИУТУгЮЯпТЗУПдТгЮПЭШЫЪ§ПижЦдк200ШЫвдФкЃЌИУТУгЮЯпТЗБЈМлЕФШЁжЕЗЖЮЇЮЊ1100дЊ/ШЫ~1200дЊ/ШЫжЎМфЃЛ
ЃЈ2ЃЉ![]() ЃЌ
ЃЌ![]() ЃЌЁр
ЃЌЁр![]()
Ёп![]() ЃЌЁрЕБ
ЃЌЁрЕБ![]() ЪБЃЌzзюЕЭЃЌМД
ЪБЃЌzзюЕЭЃЌМД![]() ЃЛ
ЃЛ
ЃЈ3ЃЉРћШѓ![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() .
.
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
23
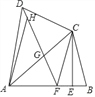
ЁОЬтФПЁПвбжЊЫФБпаЮABCDжаЃЌAB=ADЃЌЖдНЧЯпACЦНЗжЁЯDABЃЌЙ§ЕуCзїCEЁЭABгкЕуEЃЌЕуFЮЊABЩЯвЛЕуЃЌЧвEF=EBЃЌСЌНгDFЃЎ
ЃЈ1ЃЉЧѓжЄЃКCD=CFЃЛ
ЃЈ2ЃЉСЌНгDFЃЌНЛACгкЕуGЃЌЧѓжЄЃКЁїDGCЁзЁїADCЃЛ
ЃЈ3ЃЉШєЕуHЮЊЯпЖЮDGЩЯвЛЕуЃЌСЌНгAHЃЌШєЁЯADC=2ЁЯHAGЃЌAD=3ЃЌDC=2ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉжЄУїМћНтЮіЃЛЃЈ3ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЧѓГіЁЯDAC=ЁЯBACЃЌИљОнШЋЕШШ§НЧаЮЕФХаЖЈЕУГіЁїADCЁеЁїABCЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУГіCD=CBМДПЩЃЛ
ЃЈ2ЃЉИљОнШЋЕШШ§НЧаЮЕФаджЪЕУГіЁЯADC=ЁЯBЃЌЧѓГіЁЯADC+ЁЯAFC=180ЁуЃЌЁЯDCF+ЁЯDAF=180ЁуЃЌЧѓГіЁЯCDG=ЁЯDACЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪЕУГіМДПЩЃЛ
ЃЈ3ЃЉИљОнЯрЫЦШ§НЧаЮЕФаджЪЕУГіЁЯDGC=ЁЯADCЃЌ ![]() ЃЌЧѓГіЁЯHAG=ЁЯAHGЃЌ
ЃЌЧѓГіЁЯHAG=ЁЯAHGЃЌ ![]() ЃЌИљОнЯрЫЦШ§НЧаЮЕФХаЖЈЕУГіЁїDGCЁоЁїAGFЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪЕУГіМДПЩЃЎ
ЃЌИљОнЯрЫЦШ§НЧаЮЕФХаЖЈЕУГіЁїDGCЁоЁїAGFЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪЕУГіМДПЩЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉжЄУїЃКЁпACЦНЗжЁЯDABЃЌ
ЁрЁЯDAC=ЁЯBACЃЌ
дкЁїADCКЭЁїABCжа
ЁрЁїADCЁеЁїABCЃЌ
ЁрCD=CBЃЌ
ЁпCEЁЭABЃЌEF=EBЃЌ
ЁрCF=CBЃЌ
ЁрCD=CFЃЛ
ЃЈ2ЃЉЁпЁїADCЁеЁїABCЃЌ
ЁрЁЯADC=ЁЯBЃЌ
ЁпCF=CBЃЌ
ЁрЁЯCFB=ЁЯBЃЌ
ЁрЁЯADC=ЁЯCFBЃЌ
ЁрЁЯADC+ЁЯAFC=180ЁуЃЌ
ЁпЫФБпаЮAFCDЕФФкНЧКЭЕШгк360ЁуЃЌ
ЁрЁЯDCF+ЁЯDAF=180ЁуЃЌ
ЁпCD=CFЃЌ
ЁрЁЯCDG=ЁЯCFDЃЌ
ЁпЁЯDCF+ЁЯCDF+ЁЯCFD=180ЁуЃЌ
ЁрЁЯDAF=ЁЯCDF+ЁЯCFD=2ЁЯCDGЃЌ
ЁпЁЯDAB=2ЁЯDACЃЌ
ЁрЁЯCDG=ЁЯDACЃЌ
ЁпЁЯDCG=ЁЯACDЃЌ
ЁрЁїDGCЁзЁїADCЃЛ
ЃЈ3ЃЉЁпЁїDGCЁзЁїADCЃЌ
ЁрЁЯDGC=ЁЯADCЃЌ ![]() ЃЌ
ЃЌ
ЁпЁЯADC=2ЁЯHAGЃЌAD=3ЃЌDC=2ЃЌ
ЁрЁЯHAG=![]() ЁЯDGCЃЌ
ЁЯDGCЃЌ ![]() ЃЌ
ЃЌ
ЁрЁЯHAG=ЁЯAHGЃЌ ![]() ЃЌ
ЃЌ
ЁрHG=AGЃЌ
ЁпЁЯGDC=ЁЯDAC=ЁЯFAGЃЌЁЯDGC=ЁЯAGFЃЌ
ЁрЁїDGCЁоЁїAGFЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГЌЪаЯњЪлгЃЬвЃЌвбжЊгЃЬвЕФНјМлЮЊ15дЊ/ЧЇПЫЃЌШчЙћЪлМлЮЊ20дЊ/ЧЇПЫЃЌФЧУДУПЬьПЩЪлГі250ЧЇПЫЃЌШчЙћЪлМлЮЊ25дЊ/ЧЇПЫЃЌФЧУДУПЬьПЩЪлГі200ЧЇПЫЃЌОЕїВщЗЂЯжЃКУПЬьЕФЯњЪлСПyЃЈЧЇПЫЃЉгыЪлМлxЃЈдЊ/ЧЇПЫЃЉжЎМф ДцдквЛДЮКЏЪ§ЙиЯЕЃЎ
ЃЈ1ЃЉЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉШєИУГЌЪаУПЬьвЊЛёЕУРћШѓ810дЊЃЌЭЌЪБгжвЊШУЯћЗбепЕУЕНЪЕЛнЃЌдђЪлМлxгІЖЈгкЖрЩйдЊЃП
ЃЈ3ЃЉШєгЃЬвЕФЪлМлВЛЕУИпгк28дЊ/ЧЇПЫЃЌЧыЮЪЪлМлЖЈЮЊЖрЩйЪБЃЌИУГЌЪаУПЬьЯњЪлгЃЬвЫљЛёЕФРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЇаЃзМБИЙКНјвЛХњНкФмЕЦЃЌвбжЊ1жЛAаЭНкФмЕЦКЭ3жЛBаЭНкФмЕЦЙВаш26дЊЃЛ3жЛAаЭНкФмЕЦКЭ2жЛBаЭНкФмЕЦЙВаш29дЊЁЃ
ЃЈ1ЃЉЧѓ1жЛAаЭНкФмЕЦКЭ1жЛBаЭНкФмЕЦЕФЪлМлИїЪЧЖрЩйдЊЃП
ЃЈ2ЃЉбЇаЃзМБИЙКНјетСНжжаЭКХЕФНкФмЕЦЙВ80жЛЃЌВЂЧвAаЭНкФмЕЦЕФЪ§СПВЛЖргкBаЭНкФмЕЦЕФ3БЖЃЌЮЪШчКЮЙКТђзюЪЁЧЎЃЌЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
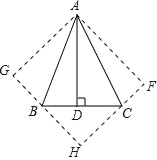
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯBAC=45ЁуЃЌADЁЭBCгкDЃЌНЋЁїACDбиACелЕўЮЊЁїACFЃЌНЋЁїABDбиABелЕўЮЊЁїABGЃЌбгГЄFCКЭGBЯрНЛгкЕуHЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮAFHGЮЊе§ЗНаЮЃЛ
ЃЈ2ЃЉШєBD=6ЃЌCD=4ЃЌЧѓABЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
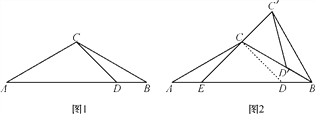
ЁОЬтФПЁПШчЭМ1ЃЌЁїABCжаЃЌACЃНBCЃЌЁЯAЃН30ЁуЃЌЕуDдкABБпЩЯЃЌЧвЁЯADCЃН45Ёу.
(1)ЧѓЁЯBCDЕФЖШЪ§ЃЛ
(2)НЋЭМ1жаЕФЁїBCDШЦЕуBЫГЪБеыа§зЊЕУЕНЁїBCЁфDЁфЃЌЕБЕуDЁфЧЁКУТфдкBCБпЩЯЪБЃЌШчЭМ2ЫљЪОЃЌСЌНгCЁфCВЂбгГЄНЛABгкЕуE.
ЂйЧѓЁЯCЁфCBЕФЖШЪ§ЃЛ
ЂкЧѓжЄЃКЁїCЁфBDЁфЁеЁїCAE.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЯТБэЃЌДгзѓБпЕк1ИіИёзгПЊЪМвРДЮдкУПИіИёзгжаЬюШывЛИіе§ећЪ§ЃЌЕк1ИіИёзгЬюШы![]() ЃЌЕк2ИіИёзгЬюШы
ЃЌЕк2ИіИёзгЬюШы![]() ЃЌЕк3ИіИёзгЬюШы
ЃЌЕк3ИіИёзгЬюШы![]() ЃЌЁЃЌЕкnИіИёзгЬюШы
ЃЌЁЃЌЕкnИіИёзгЬюШы![]() ЃЌвдДЫРрЭЦ. БэжаШЮвт4ИіЯрСкИёзгжаЫљЬюе§ећЪ§жЎКЭЖМЯрЕШЃЌЦфжа
ЃЌвдДЫРрЭЦ. БэжаШЮвт4ИіЯрСкИёзгжаЫљЬюе§ећЪ§жЎКЭЖМЯрЕШЃЌЦфжа![]() ЃЎ
ЃЎ
|
|
|
| Ё |
| Ё |
ЃЈ1ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЃЛ
ЃЛ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉНЋБэжаЧА2020ИіЪ§ЕФКЭМЧЮЊSЃЌШє![]() ЃЌЧѓSЕФжЕЃЎ
ЃЌЧѓSЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫМгЧПЙЋУёЕФНкЫЎвтЪЖ,КЯРэРћгУЫЎзЪдДЃЌЮвЪаВЩгУМлИёЕїПиЕФЪжЖЮДяЕННкЫЎЕФФПЕФЃЌЮвЪаздРДЫЎЪеЗбЕФМлФПБэШчЯТБэЃК
МлФПБэ | |
УПдТгУЫЎСП | ЕЅМл |
ВЛГЌГі6m3ЕФВПЗж | 3дЊ/m3 |
ГЌГі6m3ВЛГЌГі10m3ЕФВПЗж | 5дЊ/m3 |
ГЌГі10m3ЕФВПЗж | 9дЊ/m3 |
зЂЃКЫЎЗбАДдТНсЫу | |
ЧыИљОнШчБэЕФФкШнНтД№ЯТСаЮЪЬтЃК
(1)ЬюПеЃКШєИУЛЇОгУё2дТЗнгУЫЎ4m3ЃЌдђгІЪеЫЎЗб_______дЊЃЛ
(2)ШєИУЛЇОгУё3дТЗнгУЫЎam3(Цфжа6m3<a<10m3)ЃЌдђгІЪеЫЎЗбЖрЩйдЊ?(гУКЌaЕФДњЪ§ЪНБэЪОЃЌВЂЛЏМђ)
(3)ШєИУЛЇОгУё4ЁЂ5СНИідТЙВгУЫЎ15m3(5дТЗнгУЫЎСПГЌЙ§СЫ4дТЗн),Щш4дТЗнгУЫЎxm3ЃЌЧѓИУЛЇОгУё4ЁЂ5СНИідТЙВНЛЫЎЗбЖрЩйдЊ?(гУКЌxЕФДњЪ§ЪНБэЪОЃЌВЂЛЏМђ)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯC=90ЁуЃЎ
ЃЈ1ЃЉгУдВЙцКЭжБГпдкACЩЯзїЕуPЃЌЪЙЕуPЕНAЁЂBЕФОрРыЯрЕШЃЎЃЈБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈКЭжЄУїЃЉ
ЃЈ2ЃЉЕБТњзуЃЈ1ЃЉЕФЕуPЕНABЁЂBCЕФОрРыЯрЕШЪБЃЌЧѓЁЯAЕФЖШЪ§ЃЎ
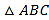
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
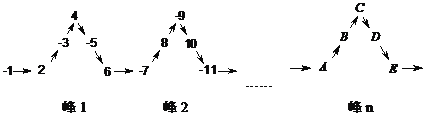
ЁОЬтФПЁПНЋвЛСагаРэЪ§-1ЃЌ2ЃЌ-3ЃЌ4ЃЌ-5ЃЌ6ЃЌЁЁЃЌШчЭМЫљЪОгаађХХСа.ИљОнЭМжаЕФХХСаЙцТЩПЩжЊЃЌЁАЗх1ЁБжаЗхЖЅЕФЮЛжУ(CЕФЮЛжУ)ЪЧгаРэЪ§4.дђ-2019гІХХдкAЃЌBЃЌCЃЌDЃЌEжа______ЕФЮЛжУ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com