
【题目】为了加强公民的节水意识,合理利用水资源,我市采用价格调控的手段达到节水的目的,我市自来水收费的价目表如下表:
价目表 | |
每月用水量 | 单价 |
不超出6m3的部分 | 3元/m3 |
超出6m3不超出10m3的部分 | 5元/m3 |
超出10m3的部分 | 9元/m3 |
注:水费按月结算 | |
请根据如表的内容解答下列问题:
(1)填空:若该户居民2月份用水4m3,则应收水费_______元;
(2)若该户居民3月份用水am3(其中6m3<a<10m3),则应收水费多少元?(用含a的代数式表示,并化简)
(3)若该户居民4、5两个月共用水15m3(5月份用水量超过了4月份),设4月份用水xm3,求该户居民4、5两个月共交水费多少元?(用含x的代数式表示,并化简)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
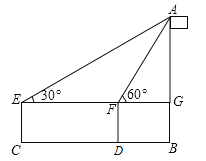
【题目】如图,小丽准备测一根旗杆AB的高度,已知小丽的眼睛离地面的距离EC=1.5米,第一次测量点C和第二次测量点D之间的距离CD=10米,∠AEG=30°,∠AFG=60°,请你帮小丽计算出这根旗杆的高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社推出一条成本价位500元/人的省内旅游线路,游客人数y(人/月)与旅游报价x(元/人)之间的关系为y=﹣x+1300,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
(1)要将该旅游线路每月游客人数控制在200人以内,求该旅游线路报价的取值范围;
(2)求经营这条旅游线路每月所需要的最低成本;
(3)档这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?
【答案】(1)取值范围为1100元/人~1200元/人之间;(2)50000;(3)x=900时,w最大=160000
【解析】试题分析:(1)根据题意列不等式求解可;
(2)根据报价减去成本可得到函数的解析式,根据一次函数的图像求解即可;
(3)根据利润等于人次乘以价格即可得到函数的解析式,然后根据二次函数的最值求解即可.
试题解析:(1)∵由题意得![]() 时,即
时,即![]() ,
,
∴解得![]()
即要将该旅游线路每月游客人数控制在200人以内,该旅游线路报价的取值范围为1100元/人~1200元/人之间;
(2)![]() ,
,![]() ,∴
,∴![]()
∵![]() ,∴当
,∴当![]() 时,z最低,即
时,z最低,即![]() ;
;
(3)利润![]()
当![]() 时,
时,![]() .
.
【题型】解答题
【结束】
23
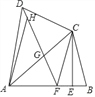
【题目】已知四边形ABCD中,AB=AD,对角线AC平分∠DAB,过点C作CE⊥AB于点E,点F为AB上一点,且EF=EB,连接DF.
(1)求证:CD=CF;
(2)连接DF,交AC于点G,求证:△DGC∽△ADC;
(3)若点H为线段DG上一点,连接AH,若∠ADC=2∠HAG,AD=3,DC=2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的大小为( )
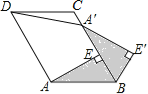
A. 130° B. 150° C. 160° D. 170°
查看答案和解析>>
科目:初中数学 来源: 题型:
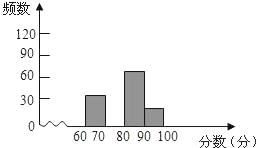
【题目】为迎接国庆60周年,某校举行以“祖国成长我成长”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成图表如下:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x<100 | 20 | 0.1 |
请根据以上图表提供的信息,解答下列问题:
(1)表中m和n所表示的数分别为:m= ,n= ;
(2)请在图中,补全频数分布直方图;
(3)比赛成绩的中位数落在哪个分数段;
(4)如果比赛成绩80分以上(含80分)可以获得奖励,那么获奖率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(m+n+1)x+m(n≥0)的两个实数根为α、β,且α≤β.
(1)试用含α、β的代数式表示m和n;
(2)求证:α≤1≤β;
(3)若点P(α,β)在△ABC的三条边上运动,且△ABC顶点的坐标分别为A(1,2)、B(![]() ,1)、C(1,1),问是否存在点P,使m+n=
,1)、C(1,1),问是否存在点P,使m+n=![]() ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
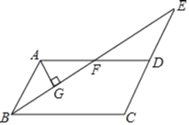
【题目】如图,在平行四边形ABCD中,∠ABC的平分线与CD的延长线交于点E,与AD交于点F,且点F恰好为边AD的中点.
(1)求证:△ABF≌△DEF;
(2)若AG⊥BE于G,BC=4,AG=1,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
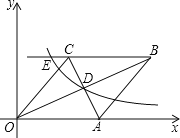
【题目】已知如图,四边形OABC为菱形,A点的坐标为![]() ,对角线OB、AC相交于D点,双曲线
,对角线OB、AC相交于D点,双曲线![]() 经过D点,交BC的延长线于E点,且
经过D点,交BC的延长线于E点,且![]() ,则E点的坐标是
,则E点的坐标是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com