
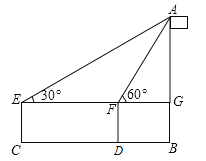
【题目】如图,小丽准备测一根旗杆AB的高度,已知小丽的眼睛离地面的距离EC=1.5米,第一次测量点C和第二次测量点D之间的距离CD=10米,∠AEG=30°,∠AFG=60°,请你帮小丽计算出这根旗杆的高度.(结果保留根号)
科目:初中数学 来源: 题型:
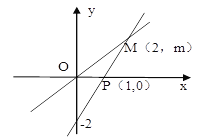
【题目】如图,一次函数y=ax+b的图像与正比例函数y=kx的图像交于点M,
(1)求正比例函数和一次函数的解析式;
(2)根据图像写出使正比例函数的值大于一次函数的值的x的取值范围;
(3)求ΔMOP的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
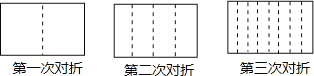
【题目】将一张长方形的纸对折,如图所示可得到一条折痕(图中虚线):继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折n次,可以得到___________条折痕.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售樱桃,已知樱桃的进价为15元/千克,如果售价为20元/千克,那么每天可售出250千克,如果售价为25元/千克,那么每天可售出200千克,经调查发现:每天的销售量y(千克)与售价x(元/千克)之间 存在一次函数关系.
(1)求y与x之间的函数关系式;
(2)若该超市每天要获得利润810元,同时又要让消费者得到实惠,则售价x应定于多少元?
(3)若樱桃的售价不得高于28元/千克,请问售价定为多少时,该超市每天销售樱桃所获的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是![]() 。
。

已知点A是数轴上的点,完成下列各题:
(1)如果点A表示的数是3,将点A先向左移动7个单位长度,再向右移动5个单位长度,那么终点B表示的数是__________,A、B两点间的距离为__________;
(2)如果点A表示的数是-4,将点A先向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是__________,A、B两点间的距离为__________;
(3)一般地,如果点A表示的数是m,将点A先向右移动n个单位长度,再向左移动t个单位长度,那么终点B表示的数是__________,A、B两点间的距离为__________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知张强家、体育场、文具店在同一直线上,下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.图中![]() 表示时间,
表示时间,![]() 表示张强离家的距离.
表示张强离家的距离.

根据图象解答下列问题:
(1)体育场离张强家多远?张强从家到体育场用了多少时间?
(2)体育场离文具店多远?
(3)张强在文具店停留了多少时间?
(4)求张强从文具店回家过程中![]() 与
与![]() 的函数解析式.
的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a是最大的负整数,b是-5的相反数,c=-|-2|,且a、b、c分别是点A、B、C在数轴上对应的数.
![]()
(1)求a、b、c的值,并在数轴上标出点A、B、C.
(2)若动点P从点A出发沿数轴正方向运动,动点Q同时从点B出发也沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒1个单位长度,求运动几秒后,点P可以追上点Q?
(3)在数轴上找一点M,使点M到A、B、C三点的距离之和等于12,请求出所有点M对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元。
(1)求1只A型节能灯和1只B型节能灯的售价各是多少元?
(2)学校准备购进这两种型号的节能灯共80只,并且A型节能灯的数量不多于B型节能灯的3倍,问如何购买最省钱,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,我市采用价格调控的手段达到节水的目的,我市自来水收费的价目表如下表:
价目表 | |
每月用水量 | 单价 |
不超出6m3的部分 | 3元/m3 |
超出6m3不超出10m3的部分 | 5元/m3 |
超出10m3的部分 | 9元/m3 |
注:水费按月结算 | |
请根据如表的内容解答下列问题:
(1)填空:若该户居民2月份用水4m3,则应收水费_______元;
(2)若该户居民3月份用水am3(其中6m3<a<10m3),则应收水费多少元?(用含a的代数式表示,并化简)
(3)若该户居民4、5两个月共用水15m3(5月份用水量超过了4月份),设4月份用水xm3,求该户居民4、5两个月共交水费多少元?(用含x的代数式表示,并化简)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com