
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.观察下面的点阵图和相应的等式,探究其中的规律:
(1)下图反映了任何一个三角形数是如何得到的,认真观察,并在④后面的横线上写出相应的等式;
![]()
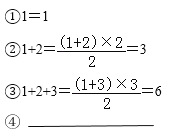
(2)通过猜想,写出(1)中与第八个点阵相对应的等式 ;
(3)从下图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.结合(1)观察下列点阵图,并在⑤看面的横线上写出相应的等式.


(4)通过猜想,写出(3)中与第n个点阵相对应的等式 ;
(5)判断256是不是正方形数,如果不是,说明理由;如果是,256可以看作哪两个相邻的“三角形数”之和?
【答案】(1)1+2+3+4=![]() =10;(2)1+2+3+…+8=
=10;(2)1+2+3+…+8=![]() ;(3)10+15=52;(4)
;(3)10+15=52;(4)![]() =n2;(5)是正方形数,可以看作是120、136两个相邻的三角形数的和.
=n2;(5)是正方形数,可以看作是120、136两个相邻的三角形数的和.
【解析】
(1)根据计算方法写出即可;
(2)根据求解规律,用点阵的序数乘比序数大1的数,再除以2即可;
(3)根据(1)中三角形数的规律写出即可;
(4)用第(n1)个三角形数加上第n个三角形数,整理即可得解;
(5)根据256=162可得是正方形数,然后再计算三角形数即可.
解:(1)④1+2+3+4=![]() =10;
=10;
(2)第八个点阵相应的等式:1+2+3+…+8=![]() ;
;
(3)⑤10+15=52;
(4)第n个点阵相对应的等式:![]() =n2;
=n2;
(5)∵256=162,
∴256是正方形数,
而1+2+3+…+16=136,1+2+3+…+15=120,
∴可以看作是120、136这两个相邻的三角形数的和.


 核心素养学练评系列答案
核心素养学练评系列答案科目:初中数学 来源: 题型:
【题目】已知在纸面上有一数轴(如图所示).
(1)操作一:折叠纸面,若表示1的点与表示-1的点重合,则表示-4的点与表示______的点重合.
(2)操作二:折叠纸面,使表示-1的点与表示3的点重合,回答以下问题:
①表示5的点与表示______的点重合.
②数轴上A,B两点之间的距离为13(点A在点B的左侧),且A,B两点经折叠后重合,求两点表示的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
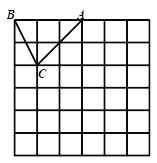
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.
(1)在网格中画出△A1B1C1和△A1B2C2;
(2)计算线段AC从开始变换到A1 C2的过程中扫过区域的面积(重叠部分不重复计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
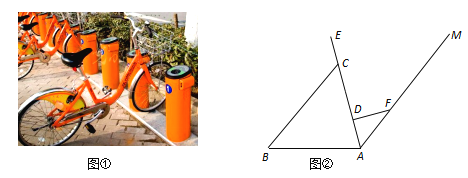
【题目】“低碳环保,你我同行”.近几年,各大城市的公共自行车给市民出行带来了极大的方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A.D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() O
O![]() 中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线
中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线![]() 和
和![]() 轴上.已知C1(1,-1),C2(
轴上.已知C1(1,-1),C2(![]() ,
, ![]() ),则点A3的坐标是________________________.
),则点A3的坐标是________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
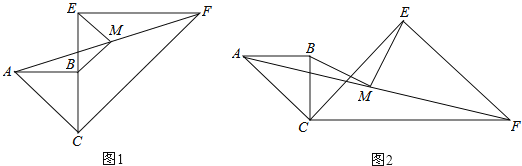
(1)如图1,当CB与CE在同一直线上时,求证:MB∥CF;
(2)如图1,若CB=a,CE=2a,求BM,ME的长;
(3)如图2,当∠BCE=45°时,求证:BM=ME.
查看答案和解析>>
科目:初中数学 来源: 题型:
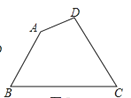
【题目】如图,现有一块四边形的木板余料ABCD,经测量AB=25cm,BC=54cm,CD=30cm,且tanB=tanC=![]() ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,则该矩形的面积为____________.
,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,则该矩形的面积为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
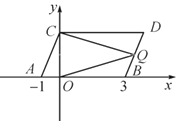
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D.连接AC,BD.
(1)写出点C,D的坐标及四边形ABDC的面积.
(2)在y轴上是否存在一点P,连接PA,PB,使S三角形PAB=S四边形ABDC?若存在,求出点P的坐标,若不存在,试说明理由;
(3)点Q是线段BD上的动点,连接QC,QO,当点Q在BD上移动时(不与B,D重合),给出下列结论:①![]() 的值不变;②
的值不变;②![]() 的值不变,其中有且只有一个正确,请你找出这个结论并求值.
的值不变,其中有且只有一个正确,请你找出这个结论并求值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com