
����Ŀ�������龳:��ֱ��AB��һ��OΪ�˵�������OM��ON����һ��ֱ�������ε�ֱ�Ƕ������O��(��COD=90��).
(1)��ͼ1��ֱ�����ǰ�COD�ı�OD��������OB�ϣ�OMƽ�֡�AOC��ON��OB�غϣ����MON=_����
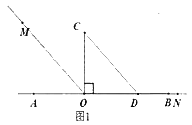
(2)ֱ�����ǰ�COD�Ƶ�O��ת����ͼ2��λ�ã�OMƽ�֡�AOC��ONƽ�֡�BOD�����MON�Ķ�����
(3)ֱ�����ǰ�COD�Ƶ�O��ת����ͼ3��λ�ã�OMƽ�֡� AOC ��ONƽ�֡�BOD�������MON�Ķ�������˵�����ɡ�
���𰸡���1��135��
��2����MON=135��
��3��������MON=135����֤��������.
��������
��1���������COM=45������������MON=��COM+��CON���������
��2���������AOC+��BOD=90�����ٸ���OMƽ����AOC��ONƽ����BOD����֪��COM+��DON=45������������MON=��COM+��DON+��COD���������
��3����ͼ�ӳ�NO��Q��DO��H������DOHΪƽ�ǣ���COH=90�������ݶԶ�����ȣ�֪��BOD=��AOH����NOD=��QOH���ٸ��ݡ�COH=��AOC-��AOH=90������OMƽ����AOC��ONƽ����BOD������COM-��QOH=45��������MON=��COD-��NOD+��COM=��COD+��COM-��QOH=90��+45��=135��.
��1���ߡ�AOC=90����OMƽ�֡�AOC��
����COM=45����
����MON=��COM+��CON=45��+90��=135����
��2���ߡ�COD=90����
����AOC+��BOD=90����
��OMƽ����AOC��ONƽ����BOD��
����COM+��DON=![]() ����AOC+��BOD��=45����
����AOC+��BOD��=45����
����MON=��COM+��DON+��COD=45��+90��=135����
��3��������MON=135����֤�����£�
��ͼ�ӳ�NO��Q��DO��H��
����DOHΪƽ�ǣ���COH=90����
���COH=��AOC-��AOH=90����
���ߡ�BOD=��AOH����NOD=��QOH��
OMƽ����AOC��ONƽ����BOD��
����COM-��QOH=45����
����MON=��COD-��NOD+��COM
=��COD+��COM-��QOH
=90��+45��=135��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����![]() �У�
�� ![]() ��
��
��1�������� ![]() �Ľ�ƽ����
�Ľ�ƽ����![]() ��Ҫ�߹���ͼ����д������������ͼ�ۼ���;
��Ҫ�߹���ͼ����д������������ͼ�ۼ���;
��2���ڣ�1���������£���![]() ��
�� ![]() ����
����![]() �ij���
�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A�ں���y1=�� ![]() ��x��0����ͼ���ϣ���B��ֱ��y2=kx+1+k��kΪ��������k��0���ϣ���A��B�������ԭ��Գƣ���Ƶ�A��BΪ����y1 �� y2ͼ���ϵ�һ�ԡ��Ѻõ㡱����������������ͼ���ϵġ��Ѻõ㡱���������Ϊ�� ��
��x��0����ͼ���ϣ���B��ֱ��y2=kx+1+k��kΪ��������k��0���ϣ���A��B�������ԭ��Գƣ���Ƶ�A��BΪ����y1 �� y2ͼ���ϵ�һ�ԡ��Ѻõ㡱����������������ͼ���ϵġ��Ѻõ㡱���������Ϊ�� ��
A.��1�Ի�2��
B.ֻ��1��
C.ֻ��2��
D.��2�Ի�3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=![]() x+2��x���ڵ�A����y���ڵ�B����P��x��y�����߶�AB��һ���㣨��A��B���غϣ�����PAO�����ΪS����S��x�ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ.
x+2��x���ڵ�A����y���ڵ�B����P��x��y�����߶�AB��һ���㣨��A��B���غϣ�����PAO�����ΪS����S��x�ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
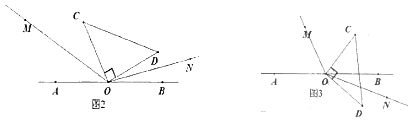
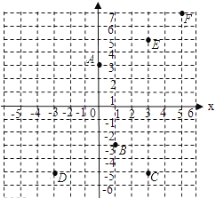
����Ŀ����ƽ��ֱ�������б�ʾ�������:A��0��3����B��1����3����C��3����5����D����3����5����E��3��5����F��5��7��.
��A�㵽ԭ��O�ľ�����________ ��
������C��x��ĸ�����ƽ��6����λ�����________�غϣ�
������CE����ֱ��CE��y��λ�ù�ϵ��________ ��
����F�ֱ�x��y��ľ���ֱ���________ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A�Ƿ���������y=�� ![]() ��ͼ���ϵ�һ�����㣬����OA�������߶�O A�Ƶ�O˳ʱ����ת90��õ��߶�OB�����B����ͼ��ĺ�������ʽΪ ��
��ͼ���ϵ�һ�����㣬����OA�������߶�O A�Ƶ�O˳ʱ����ת90��õ��߶�OB�����B����ͼ��ĺ�������ʽΪ �� 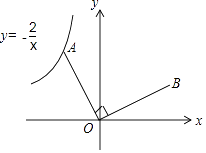
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�P��CD����һ�㣬��AP��BP�ֱ�ƽ�֡�DAB�͡�CBA����AD=5��AP=8�����APB���ܳ��� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
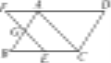
����Ŀ����ͼ������ABCD�У���E�ڱ�BC�ϣ���F�ڱ�DA���ӳ����ϣ���AF��CE��EF��AB���ڵ�G.
(1)��֤��AC��EF��
(2)����G��AB���е㣬BE��6�����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ǹ涨���ǡ�![]() ����ʾΪ��abc������
����ʾΪ��abc������![]() ����ʾΪ����xm+yn�������磺
����ʾΪ����xm+yn�������磺![]() =1��19��3�£�24+31��=3�����������涨����������⣺
=1��19��3�£�24+31��=3�����������涨����������⣺
��1�����㣺![]() = ______ ��
= ______ ��
��2������ʽ Ϊ��ȫƽ��ʽ����k= ______ ��
Ϊ��ȫƽ��ʽ����k= ______ ��
��3���ⷽ�̣�![]() =6x2+7��
=6x2+7��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com