
【题目】如图,已知点A是反比例函数y=﹣ ![]() 的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为 .
的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为 . 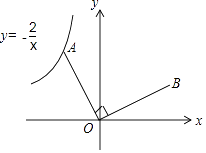
科目:初中数学 来源: 题型:
【题目】某商店用 500 元购进 A、B 两种铅笔盒共 50 个,这两种铅笔盒的进价、标价如下表所示.
类型 价格 | A 型 | B 型 |
进价(元/个) | 8 | 13 |
标价(元/个) | 12 | 20 |
(1)这两种笔记本各购进多少个?
(2)若 A 型笔记本按标价的 9 折出售,B 型笔记本按标价的 8 折出售,那么这批笔记本 全部售出后,商店共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
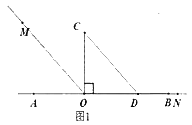
【题目】问题情境:以直线AB上一点O为端点作射线OM、ON,将一个直角三角形的直角顶点放在O处(∠COD=90°).
(1)如图1,直角三角板COD的边OD放在射线OB上,OM平分∠AOC,ON和OB重合,则∠MON=_°;
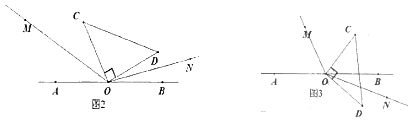
(2)直角三角板COD绕点O旋转到如图2的位置,OM平分∠AOC,ON平分∠BOD,求∠MON的度数。
(3)直角三角板COD绕点O旋转到如图3的位置,OM平分∠ AOC ,ON平分∠BOD,猜想∠MON的度数,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两工程队承包一项工程,如果甲工程队单独施工,恰好如期完成;如果乙工程队单独施工就要超过6个月才能完成,现在甲、乙两队先共同施工4个月,剩下的由乙队单独施工,则恰好如期完成.
(1)问原来规定修好这条公路需多少长时间?
(2)现要求甲、乙两个工程队都参加这项工程,但由于受到施工场地条件限制,甲、乙两工程队不能同时施工.已知甲工程队每月的施工费用为4万元,乙工程队每月的施工费用为2万元.为了结算方便,要求:甲、乙的施工时间为整数个月,不超过15个月完成.当施工费用最低时,甲、乙各施工了多少个月?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B、C、D是正方形网格纸上的四个格点,根据要求在网格中画图并标注相关字母.
①画线段AB;
②画射线CA、直线AD;
③过点B画AD的平行线BE;
④过点D画AC的垂线,垂足为F.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若我们规定三角“![]() ”表示为:abc;方框“
”表示为:abc;方框“![]() ”表示为:(xm+yn).例如:
”表示为:(xm+yn).例如:![]() =1×19×3÷(24+31)=3.请根据这个规定解答下列问题:
=1×19×3÷(24+31)=3.请根据这个规定解答下列问题:
(1)计算:![]() = ______ ;
= ______ ;
(2)代数式 为完全平方式,则k= ______ ;
为完全平方式,则k= ______ ;
(3)解方程:![]() =6x2+7.
=6x2+7.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com