
【题目】如图,已知正方形ABCD,把边DC绕D点顺时针旋转30°到DC′处,连接AC′,BC′,CC′,写出图中所有的等腰三角形,并写出推理过程.
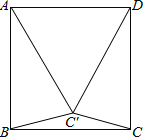
【答案】△DCC′,△DC′A,△C′AB,△C′BC,理由见解析.
【解析】
试题利用旋转的性质以及正方形的性质进而得出等腰三角形,再利用全等三角形的判定与性质判断得出.
试题解析:图中的等腰三角形有:△DCC′,△DC′A,△C′AB,△C′BC,理由如下:
∵四边形ABCD是正方形,∴AB=AD=DC,∠BAD=∠ADC=90°.∴DC=DC′=DA.
∴△DCC′,△DC′A为等腰三角形.
∵∠C′DC=30°,∠ADC=90°,∴∠ADC′=60°.∴△AC′D为等边三角形.
∵∠C′AB=90°-60°=30°,∴∠CDC′=∠C′AB.
在△DCC′和△AC′B中CD=BA,∠CDC′=∠C′AB,C′D=C′A,
∴△DCC′≌△AC′B(SAS).∴CC′=C′B,∴△BCC′为等腰三角形.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在AB,AD上,且BE=AF,连接CE,BF相交于点G,则下列结论不正确的是( )
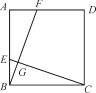
A. BF=CE B. ∠AFB=∠ECD C. BF⊥CE D. ∠AFB+∠BEC=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+2交x轴于点A,交y轴于点B,点P(x,y)是线段AB上一动点(与A,B不重合),△PAO的面积为S,求S与x的函数关系式,并写出自变量的取值范围.
x+2交x轴于点A,交y轴于点B,点P(x,y)是线段AB上一动点(与A,B不重合),△PAO的面积为S,求S与x的函数关系式,并写出自变量的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是反比例函数y=﹣ ![]() 的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为 .
的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为 . 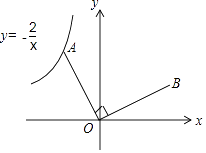
查看答案和解析>>
科目:初中数学 来源: 题型:
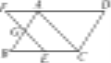
【题目】如图,在□ABCD中,点E在边BC上,点F在边DA的延长线上,且AF=CE,EF与AB交于点G.
(1)求证:AC∥EF;
(2)若点G是AB的中点,BE=6,求边AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC三个顶点都在格点上,点A、B、C的坐标分别为A(﹣1,3),B(﹣3,1),C(﹣1,1).请解答下列问题: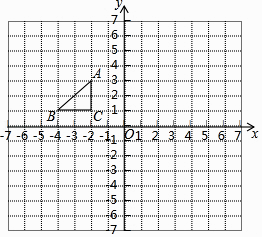
(1)画出△ABC关于y轴对称的△A1B1C1 , 并写出B1的坐标.
(2)画出△A1B1C1绕点C1顺时针旋转90°后得到的△A2B2C1 , 并求出点A1走过的路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com