
【题目】如图,在正方形ABCD中,点E,F分别在AB,AD上,且BE=AF,连接CE,BF相交于点G,则下列结论不正确的是( )
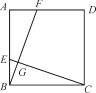
A. BF=CE B. ∠AFB=∠ECD C. BF⊥CE D. ∠AFB+∠BEC=90°
【答案】D
【解析】
根据已知条件易证△ABF≌△BCE,由全等三角形的性质可得BF=CE,∠AFB=∠BEC,故A正确;由AB∥CD,得∠BEC=∠ECD,可以判断B正确;再由∠AFB+∠ABF=90°,推出∠BEG+∠EBG=90°即可判断选项C正确;根据已知条件,选项D无法证明,选项D 错误.
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠ABC=90°,
在△ABF和△BCE中,
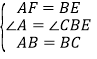 ,
,
∴△ABF≌△BCE,
∴BF=CE,∠AFB=∠BEC,选项A正确,
∵AB∥CD,
∴∠BEC=∠ECD,
∴∠AFB=∠ECD,选项B正确,
∵∠AFB+∠ABF=90°,
∴∠BEG+∠EBG=90°,
∴∠EGB=90°,
∴BF⊥EC,选项C正确,
根据已知条件,选项D无法证明,选项D 错误.
故选D.


科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,点O是△ABC的中心,∠FOG=120°,绕点O旋转∠FOG,分别交线段AB,BC于D,E两点,连接DE,给出下列三个结论①OD=OE; ②S△ODE=S△BDE;③四边形ODBE的面积始终等于![]() .述结论中正确的个数是( )
.述结论中正确的个数是( )

A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D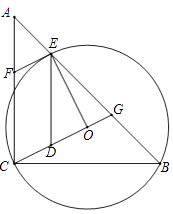
(1)求证:四边形CDEF是平行四边形;
(2)若BC=3,tan∠DEF=2,求BG的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线交于点O,以AD为边向外作Rt△ADE,∠AED=90°,连接OE,DE=6,OE=8 ![]() ,则另一直角边AE的长为 .
,则另一直角边AE的长为 . 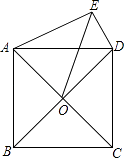
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①为北斗七星的位置图,图②将北斗七星分别标为A,B,C,D,E,F,G,将A,B,C,D,E,F顺次首尾连接,若AF恰好经过点G,且AF∥DE,∠B=∠C+10°,∠D=∠E=105°.
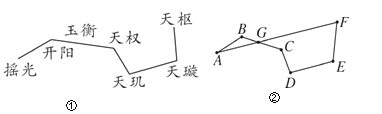
(1)求∠F的度数;
(2)计算∠B-∠CGF的度数是______;(直接写出结果)
(3)连接AD,∠ADE与∠CGF满足怎样数量关系时,BC∥AD,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com