
【题目】如图,正方形ABCD的对角线交于点O,以AD为边向外作Rt△ADE,∠AED=90°,连接OE,DE=6,OE=8 ![]() ,则另一直角边AE的长为 .
,则另一直角边AE的长为 . 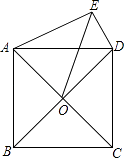
【答案】10
【解析】解:过点O作OM⊥AE于点M,作ON⊥DE,交ED的延长线于点N, 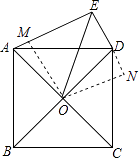
∵∠AED=90°,
∴四边形EMON是矩形,
∵正方形ABCD的对角线交于点O,
∴∠AOD=90°,OA=OD,
∴∠AOD+∠AED=180°,
∴点A,O,D,E共圆,
∴ ![]() =
= ![]() ,
,
∴∠AEO=∠DEO= ![]() ∠AED=45°,
∠AED=45°,
∴OM=ON,
∴四边形EMON是正方形,
∴EM=EN=ON,
∴△OEN是等腰直角三角形,
∵OE=8 ![]() ,
,
∴EN=8,
∴EM=EN=8,
在Rt△AOM和Rt△DON中,
![]() ,
,
∴Rt△AOM≌Rt△DON(HL),
∴AM=DN=EN﹣ED=8﹣6=2,
∴AE=AM+EM=2+8=10.
所以答案是:10.
【考点精析】本题主要考查了勾股定理的概念和圆周角定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() ,交
,交![]() 边于点
边于点![]() .
.
(1)如图1,过点![]() 作
作![]() 于
于![]() ,若已知
,若已知![]() ,求
,求![]() 的度数;
的度数;
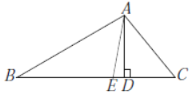
图1
(2)如图2,过点![]() 作
作![]() 于
于![]() ,若
,若![]() 恰好又平分
恰好又平分![]() ,求
,求![]() 的度数;
的度数;
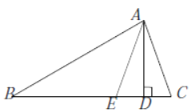
图2
(3)如图3,![]() 平分
平分![]() 的外角
的外角![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,作
,作![]() 于
于![]() ,设
,设![]() ,试求
,试求![]() 的值.(用含有
的值.(用含有![]() 的代数式表示)
的代数式表示)
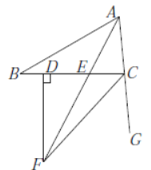
图3
(4)如图4,在图3的基础上分别作![]() 和
和![]() 的角平分线,交于点
的角平分线,交于点![]() ,作
,作![]() 于
于![]() ,设
,设![]() ,试直接写出
,试直接写出![]() 的值.(用含有
的值.(用含有![]() 的代数式表示)
的代数式表示)
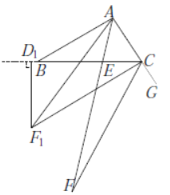
图4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
中华优秀传统文化是中华民族的“根”和“魂”,是我们必须世代传承的文化根脉、文化基因.为传承优秀传统文化,某校为各班购进《三国演义》和《水浒传》连环画若干套,其中每套《三国演义》连环画的价格比每套《水浒传》连环画的价格贵60元,用4800元购买《水浒传》连环画的套数是用3600元购买《三国演义》连环画套数的2倍,求每套《水浒传》连环画的价格.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在AB,AD上,且BE=AF,连接CE,BF相交于点G,则下列结论不正确的是( )
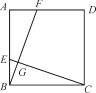
A. BF=CE B. ∠AFB=∠ECD C. BF⊥CE D. ∠AFB+∠BEC=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于点Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在x轴上,∠ABO=90°,∠A=30°,OA=4,将△OAB绕点O按顺时针方向旋转120°得到△OA′B′,则点A′的坐标是( ) 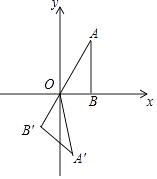
A.(2,﹣2 ![]() )
)
B.(2,﹣2 ![]() )
)
C.(2 ![]() ,2)
,2)
D.(2 ![]() ,2)
,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com