
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() ,交
,交![]() 边于点
边于点![]() .
.
(1)如图1,过点![]() 作
作![]() 于
于![]() ,若已知
,若已知![]() ,求
,求![]() 的度数;
的度数;
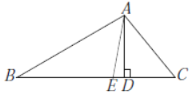
图1
(2)如图2,过点![]() 作
作![]() 于
于![]() ,若
,若![]() 恰好又平分
恰好又平分![]() ,求
,求![]() 的度数;
的度数;
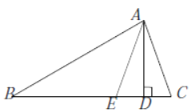
图2
(3)如图3,![]() 平分
平分![]() 的外角
的外角![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,作
,作![]() 于
于![]() ,设
,设![]() ,试求
,试求![]() 的值.(用含有
的值.(用含有![]() 的代数式表示)
的代数式表示)
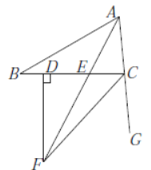
图3
(4)如图4,在图3的基础上分别作![]() 和
和![]() 的角平分线,交于点
的角平分线,交于点![]() ,作
,作![]() 于
于![]() ,设
,设![]() ,试直接写出
,试直接写出![]() 的值.(用含有
的值.(用含有![]() 的代数式表示)
的代数式表示)
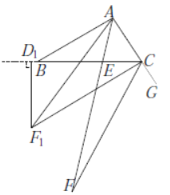
图4
【答案】(1)10°(2)70°(3)![]() =
=![]() -30°(4)
-30°(4)![]() =
=![]()
【解析】
(1)根据三角形的内角和与角平分线的性质得到∠EAC=50°,再根据直角三角形两锐角互余得到∠DAC=40°,再根据角度的和差关系即可求解;
(2)设![]() =x,根据直角三角形两锐角互余,表示出∠DAC,再表示出∠BAC,根据三角形内角和得到方程即可求出x;
=x,根据直角三角形两锐角互余,表示出∠DAC,再表示出∠BAC,根据三角形内角和得到方程即可求出x;
(3)分别用含n的式子表示出![]() ,
,![]() ,即可得到
,即可得到![]() ;
;
(4)在(3)的基础上再表示出![]() ,
,![]() ,即可得到
,即可得到![]() .
.
(1)∵![]() ,
,![]()
∴∠BAC=180°-∠B-∠C=100°
∵![]() 平分
平分![]() ,
,
∴∠EAC=![]()
![]() =50°
=50°
∵![]()
∴∠DAC=90°-∠C =40°
∴![]() =∠EAC-∠DAC=10°;
=∠EAC-∠DAC=10°;
(2)设![]() =x,
=x,
∵![]()
∴∠DAC=90°-∠C =90°-x
∵![]() 平分
平分![]() ,
,
∴![]() =2∠DAC=180°-2x
=2∠DAC=180°-2x
∵![]() 平分
平分![]() ,
,
∴![]() =2
=2![]() =360°-4x
=360°-4x
在△ABC中,![]() +∠B+∠C=180°
+∠B+∠C=180°
∴360°-4x+30°+x=180°
解得x=70°
∴![]() =70°;
=70°;
(3)∵![]() ,
,![]()
∴∠BAC=180°-∠B-![]() =150°-
=150°-![]()
∵![]() 平分
平分![]() ,
,
∴∠EAC=![]()
![]() =
=![]()
∴∠AEC=180°-∠EAC -![]() =
=![]()
∴∠DEF=∠AEC=![]()
∵![]()
∴![]() =90°-∠DEF =
=90°-∠DEF =![]() -15°
-15°
∵![]()
∴∠BCG=180°-∠ACB=180°-![]()
∵![]() 平分
平分![]()
∴∠DCF=![]()
![]() =
=![]()
∴![]() =180°-∠EAC-∠ACF=180°-∠EAC-∠ACB-∠DCF =15°
=180°-∠EAC-∠ACF=180°-∠EAC-∠ACB-∠DCF =15°
∴![]() =
=![]() -15°-15°=
-15°-15°=![]() -30°;
-30°;
(4)![]() =
=![]()
理由如下:
∵![]()
由(3)可得∠BAE =∠EAC=![]()
![]() =
=![]()
∵AF1平分∠BAE
∴∠F1AE=![]() ∠BAE =
∠BAE =![]()
由(3)同理可得![]() +
+![]() =
=![]()
又![]()
∴![]() +90°=
+90°=![]() +
+![]() +n
+n
∴![]() =
=![]()
∵CF1平分![]()
∴∠BCF1=![]() ∠BCF
∠BCF![]() ∠BCG =
∠BCG =![]()
∴![]() =180°-∠F1AC-∠ACF1=180°-∠F1AE-∠EAC-∠ACB-∠BCF1=180°-(
=180°-∠F1AC-∠ACF1=180°-∠F1AE-∠EAC-∠ACB-∠BCF1=180°-(![]() )-(
)-(![]() )-
)-![]() -(
-(![]() )=22.5°
)=22.5°
∴![]() =
=![]() -22.5°=
-22.5°=![]()
故![]() =
=![]() .
.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】目前,我国大约有1.3亿高血压病患者,预防高血压不容忽视,“千帕![]() ”和“毫米汞柱
”和“毫米汞柱![]() ”都是表示血压的单位,请你根据表格提供的信息判断,下列各组换算正确的是( )
”都是表示血压的单位,请你根据表格提供的信息判断,下列各组换算正确的是( )
千帕 | … | 10 | 12 | 14 | … |
毫米汞柱 | … | 75 | 90 | 105 | … |
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下面例题,解答问题
例题:已知二次三项式x2﹣4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得x2﹣4x+m=(x+3)(x+n),
则x2﹣4x+m=x2+(n+3)x+3n
∴![]()
解得:n=﹣7,m=﹣21.
∴另一个因式为(x﹣7),m的值为﹣21.
问题:
(1)若二次三项式x2﹣5x+6可分解为(x﹣2)(x+a),则a= ;
(2)若二次三项式2x2+bx﹣5可分解为(2x﹣1)(x+5),则b= ;
(3)仿照以上方法解答下面问题:若二次三项式2x2+3x﹣k有一个因式是(2x﹣5),求另一个因式以及k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列解题过程的空白处填上适当的内容(推理的理由或数据).
如图,![]() ,
,![]() ,
,![]() ,那么
,那么![]() 吗?说明理由.
吗?说明理由.
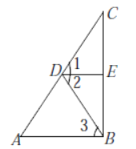
解:![]() ,理由如下:
,理由如下:
因为![]() ,
,![]() (已知)
(已知)
所以![]()
所以![]() (__________________
(__________________![]() ).
).
所以![]() (_________________________________).
(_________________________________).
所以![]() (__________________________________).
(__________________________________).
![]() (______________________________________).
(______________________________________).
因为![]() ,
,
所以![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,点O是△ABC的中心,∠FOG=120°,绕点O旋转∠FOG,分别交线段AB,BC于D,E两点,连接DE,给出下列三个结论①OD=OE; ②S△ODE=S△BDE;③四边形ODBE的面积始终等于![]() .述结论中正确的个数是( )
.述结论中正确的个数是( )

A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,线段a,b,c,d的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有( ) 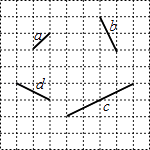
A.3种
B.6种
C.8种
D.12种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8。则图中阴影部分的面积是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
(1)求线段CD对应的函数表达式;
(2)求E点的坐标,并解释E点的实际意义;
(3)若已知轿车比货车晚出发20分钟,且到达乙地后在原地等待货车,在两车相遇后当货车和轿车相距30千米时,求货车所用时间.

考点:一次函数的应用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线交于点O,以AD为边向外作Rt△ADE,∠AED=90°,连接OE,DE=6,OE=8 ![]() ,则另一直角边AE的长为 .
,则另一直角边AE的长为 . 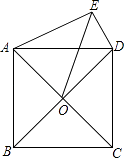
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com