
【题目】如图,等边三角形ABC的边长为4,点O是△ABC的中心,∠FOG=120°,绕点O旋转∠FOG,分别交线段AB,BC于D,E两点,连接DE,给出下列三个结论①OD=OE; ②S△ODE=S△BDE;③四边形ODBE的面积始终等于![]() .述结论中正确的个数是( )
.述结论中正确的个数是( )

A. 3 B. 2 C. 1 D. 0
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点0是坐标原点.边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,点E是对角线AC上一点,连接OE、BE,BE的延长线交OA于点P,若△OCE的面积为12.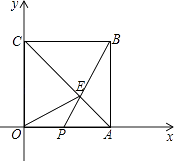
(1)求点E的坐标:
(2)求△OPE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【新知理解】
如图①,点C在线段AB上,图中共有三条线段AB、AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“巧点”.
线段的中点__________这条线段的“巧点”;(填“是”或“不是”).
若AB = 12cm,点C是线段AB的巧点,则AC=___________cm;
【解决问题】
(3) 如图②,已知AB=12cm.动点P从点A出发,以2cm/s的速度沿AB向点B匀速移动:点Q从点B出发,以1cm/s的速度沿BA向点A匀速移动,点P、Q同时出发,当其中一点到达终点时,运动停止,设移动的时间为t(s).当t为何值时,A、P、Q三点中其中一点恰好是另外两点为端点的线段的巧点?说明理由

![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
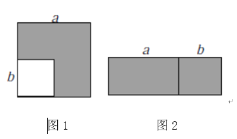
【题目】(知识情境)通常情况下,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.
(1)如图1,在边长为![]() 的正方形中挖掉一个边长为
的正方形中挖掉一个边长为![]() 的小正方形
的小正方形![]() .把余下的部分剪拼成一个长方形(如图2).通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是______________;
.把余下的部分剪拼成一个长方形(如图2).通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是______________;
(拓展探究)类似地,用两种不同的方法计算同一个几何体的体积,也可以得到一个恒等式.
如图3是边长为![]() 的正方体,被如图所示的分割线分成
的正方体,被如图所示的分割线分成![]() 块.
块.
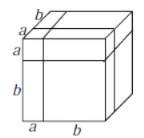
图3
(2)用不同的方法计算这个正方体的体积,就可以得到一个恒等式,这个恒等式可以为:
_________________________________________________________________;
(3)已知![]() ,
,![]() ,利用上面的恒等式求
,利用上面的恒等式求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() ,交
,交![]() 边于点
边于点![]() .
.
(1)如图1,过点![]() 作
作![]() 于
于![]() ,若已知
,若已知![]() ,求
,求![]() 的度数;
的度数;
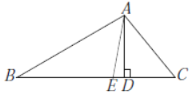
图1
(2)如图2,过点![]() 作
作![]() 于
于![]() ,若
,若![]() 恰好又平分
恰好又平分![]() ,求
,求![]() 的度数;
的度数;
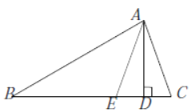
图2
(3)如图3,![]() 平分
平分![]() 的外角
的外角![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,作
,作![]() 于
于![]() ,设
,设![]() ,试求
,试求![]() 的值.(用含有
的值.(用含有![]() 的代数式表示)
的代数式表示)
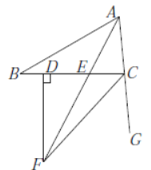
图3
(4)如图4,在图3的基础上分别作![]() 和
和![]() 的角平分线,交于点
的角平分线,交于点![]() ,作
,作![]() 于
于![]() ,设
,设![]() ,试直接写出
,试直接写出![]() 的值.(用含有
的值.(用含有![]() 的代数式表示)
的代数式表示)
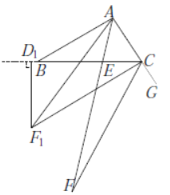
图4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OD平分∠BOF,OE⊥CD于O,若∠EOF=α,下列说法①∠AOC=α﹣90°;②∠EOB=180°﹣α;③∠AOF=360°﹣2α,其中正确的是( )
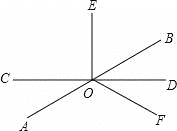
A. ①②B. ①③C. ②③D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度).
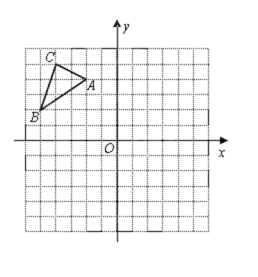
(1)在图中画出平移后的△A1B1C1;
(2)直接写出△A1B1C1各顶点的坐标
(3)求出△A1B1C1的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在AB,AD上,且BE=AF,连接CE,BF相交于点G,则下列结论不正确的是( )
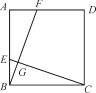
A. BF=CE B. ∠AFB=∠ECD C. BF⊥CE D. ∠AFB+∠BEC=90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com