
【题目】(知识情境)通常情况下,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.
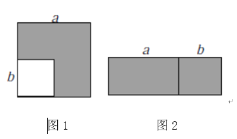
(1)如图1,在边长为![]() 的正方形中挖掉一个边长为
的正方形中挖掉一个边长为![]() 的小正方形
的小正方形![]() .把余下的部分剪拼成一个长方形(如图2).通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是______________;
.把余下的部分剪拼成一个长方形(如图2).通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是______________;
(拓展探究)类似地,用两种不同的方法计算同一个几何体的体积,也可以得到一个恒等式.
如图3是边长为![]() 的正方体,被如图所示的分割线分成
的正方体,被如图所示的分割线分成![]() 块.
块.
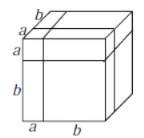
图3
(2)用不同的方法计算这个正方体的体积,就可以得到一个恒等式,这个恒等式可以为:
_________________________________________________________________;
(3)已知![]() ,
,![]() ,利用上面的恒等式求
,利用上面的恒等式求![]() 的值.
的值.
【答案】(1)a2-b2=(a+b)(a-b)(2)(a+b)3=a3+3a2b+3ab2+b3(3)40
【解析】
(1)根据平方差公式的几何验证方法即可求解;
(2)根据正方体的体积公式和给出的条件即可得出答案;
(3)根据(2)得出的式子再进行转化,然后把a+b=4,ab=2代入计算即可得出答案.
(1)图1的面积为:a2-b2, 图2的面积为(a+b)(a-b)
∴这个等式是a2-b2=(a+b)(a-b)
故答案为:a2-b2=(a+b)(a-b);
(2)图3的体积为:(a+b)3或a3+3a2b+3ab2+b3
∴这个等式是(a+b)3=a3+3a2b+3ab2+b3
故答案为:(a+b)3=a3+3a2b+3ab2+b3;
(3)由(a+b)3=a3+3a2b+3ab2+b3
得:(a+b)3=a3+3ab(a+b)+b3,
将a+b=4,ab=2代入a3+3ab(a+b)+b3
得:43=a3+3×2×4+b3,
∴a3+b3=6424=40.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】(8分) 小丽想用一块面积为400cm2的正方形纸片,沿着边的方向裁处一块面积为300cm2的长方形纸片.(1)请帮小丽设计一种可行的裁剪方案;
(2)若使长方形的长宽之比为3:2,小丽能用这块纸片裁处符合要求的纸片吗?若能,请帮小丽设计一种裁剪方案,若不能,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线 ![]() 分别与x轴、y轴交于点B、C,且与直线
分别与x轴、y轴交于点B、C,且与直线 ![]() 交于点A.
交于点A.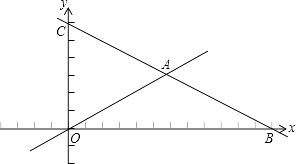
(1)分别求出点A、B、C的坐标;
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的函数表达式;
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂准备用图甲所示的A型正方形板材和B型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
![]() 若该工厂准备用不超过10000元的资金去购买A,B两种型号板材,并全部制作竖式箱子,已知A型板材每张30元,B型板材每张90元,求最多可以制作竖式箱子多少只?
若该工厂准备用不超过10000元的资金去购买A,B两种型号板材,并全部制作竖式箱子,已知A型板材每张30元,B型板材每张90元,求最多可以制作竖式箱子多少只?
![]() 若该工厂仓库里现有A型板材65张、B型板材110张,用这批板材制作两种类型的箱子,问制作竖式和横式两种箱子各多少只,恰好将库存的板材用完?
若该工厂仓库里现有A型板材65张、B型板材110张,用这批板材制作两种类型的箱子,问制作竖式和横式两种箱子各多少只,恰好将库存的板材用完?
![]() 若该工厂新购得65张规格为
若该工厂新购得65张规格为![]() 的C型正方形板材,将其全部切割成A型或B型板材
的C型正方形板材,将其全部切割成A型或B型板材![]() 不计损耗
不计损耗![]() ,用切割成的板材制作两种类型的箱子,要求竖式箱子不少于20只,且材料恰好用完,则能制作两种箱子共______只
,用切割成的板材制作两种类型的箱子,要求竖式箱子不少于20只,且材料恰好用完,则能制作两种箱子共______只![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,点O是△ABC的中心,∠FOG=120°,绕点O旋转∠FOG,分别交线段AB,BC于D,E两点,连接DE,给出下列三个结论①OD=OE; ②S△ODE=S△BDE;③四边形ODBE的面积始终等于![]() .述结论中正确的个数是( )
.述结论中正确的个数是( )

A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
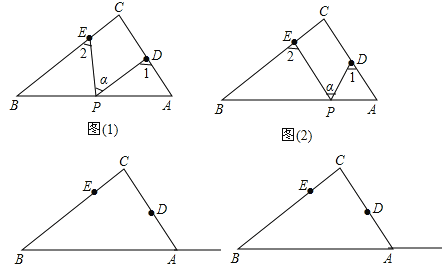
(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2= °;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间有何关系?说明理由.
(3)若点P在Rt△ABC斜边BA的延长线上运动(CE<CD),则∠α、∠1、∠2之间有何关系?猜想并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D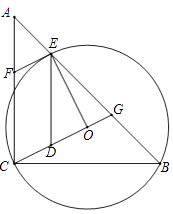
(1)求证:四边形CDEF是平行四边形;
(2)若BC=3,tan∠DEF=2,求BG的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com