
【题目】已知点A在函数y1=﹣ ![]() (x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
(x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
A.有1对或2对
B.只有1对
C.只有2对
D.有2对或3对
【答案】A
【解析】解:设A(a,﹣ ![]() ),
),
由题意知,点A关于原点的对称点B((a,﹣ ![]() ),)在直线y2=kx+1+k上,
),)在直线y2=kx+1+k上,
则 ![]() =﹣ak+1+k,
=﹣ak+1+k,
整理,得:ka2﹣(k+1)a+1=0 ①,
即(a﹣1)(ka﹣1)=0,
∴a﹣1=0或ka﹣1=0,
则a=1或ka﹣1=0,
若k=0,则a=1,此时方程①只有1个实数根,即两个函数图象上的“友好点”只有1对;
若k≠0,则a= ![]() ,此时方程①有2个实数根,即两个函数图象上的“友好点”有2对,
,此时方程①有2个实数根,即两个函数图象上的“友好点”有2对,
综上,这两个函数图象上的“友好点”对数情况为1对或2对,
故选:A.
【考点精析】根据题目的已知条件,利用求根公式和关于原点对称的点的坐标的相关知识可以得到问题的答案,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;两个点关于原点对称时,它们的坐标的符号相反,即点P(x,y)关于原点的对称点为P’(-x,-y).


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
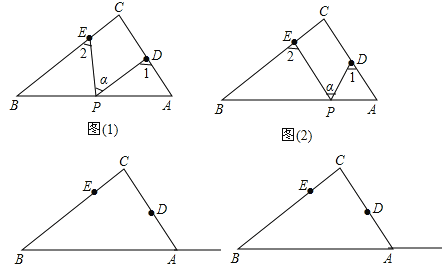
(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2= °;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间有何关系?说明理由.
(3)若点P在Rt△ABC斜边BA的延长线上运动(CE<CD),则∠α、∠1、∠2之间有何关系?猜想并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D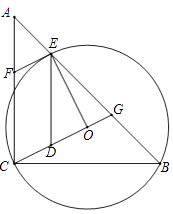
(1)求证:四边形CDEF是平行四边形;
(2)若BC=3,tan∠DEF=2,求BG的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①为北斗七星的位置图,图②将北斗七星分别标为A,B,C,D,E,F,G,将A,B,C,D,E,F顺次首尾连接,若AF恰好经过点G,且AF∥DE,∠B=∠C+10°,∠D=∠E=105°.
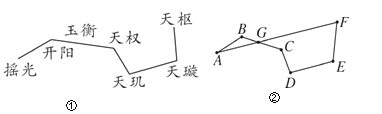
(1)求∠F的度数;
(2)计算∠B-∠CGF的度数是______;(直接写出结果)
(3)连接AD,∠ADE与∠CGF满足怎样数量关系时,BC∥AD,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
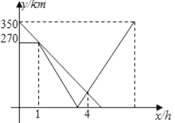
【题目】一辆货车从![]() 地匀速驶往相距350km的
地匀速驶往相距350km的![]() 地,当货车行驶1小时经过途中的
地,当货车行驶1小时经过途中的![]() 地时,一辆快递车恰好从
地时,一辆快递车恰好从![]() 地出发以另一速度匀速驶往
地出发以另一速度匀速驶往![]() 地,当快递车到达
地,当快递车到达![]() 地后立即掉头以原来的速度匀速驶往
地后立即掉头以原来的速度匀速驶往![]() 地.(货车到达
地.(货车到达![]() 地,快递车到达
地,快递车到达![]() 地后分别停止运动)行驶过程中两车与
地后分别停止运动)行驶过程中两车与![]() 地间的距离
地间的距离![]() (单位:
(单位:![]() )与货车从出发所用的时间
)与货车从出发所用的时间![]() (单位:
(单位:![]() )间的关系如图所示.则货车到达
)间的关系如图所示.则货车到达![]() 地后,快递车再行驶______
地后,快递车再行驶______![]() 到达
到达![]() 地.
地.
查看答案和解析>>
科目:初中数学 来源: 题型:
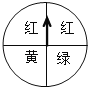
【题目】如图,有一个转盘,转盘被分成4个相同的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),求下列事件的概率:
(1)指针指向绿色;
(2)指针指向红色或黄色;
(3)指针不指向红色.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:以直线AB上一点O为端点作射线OM、ON,将一个直角三角形的直角顶点放在O处(∠COD=90°).
(1)如图1,直角三角板COD的边OD放在射线OB上,OM平分∠AOC,ON和OB重合,则∠MON=_°;
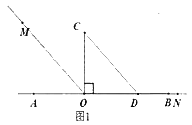
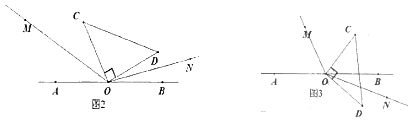
(2)直角三角板COD绕点O旋转到如图2的位置,OM平分∠AOC,ON平分∠BOD,求∠MON的度数。
(3)直角三角板COD绕点O旋转到如图3的位置,OM平分∠ AOC ,ON平分∠BOD,猜想∠MON的度数,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
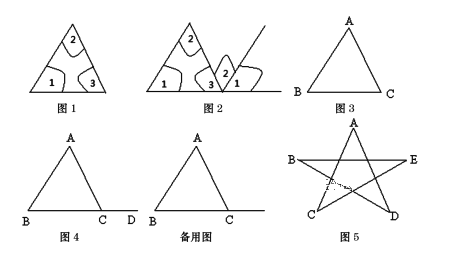
【题目】下列是某初一数学兴趣小组探究三角形内角和的过程,请根据他们的探究过程,结合所学知识,解答下列问题.兴趣小组将图1△ABC三个内角剪拼成图2,由此得△ABC三个内角的和为180度.
(1)请利用图3证明上述结论.
(2)三角形的一条边与另一条边的反向延长线组成的角,叫做三角形的外角.
如图4,点D为BC延长线上一点,则∠ACD为△ABC的一个外角.
①请探究出∠ACD与∠A、∠B的关系,并直接填空:∠ACD=______.
②如图5是一个五角星,请利用上述结论求∠A+∠B+∠C+∠D+∠E的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com