
【题目】如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.
求:(1)PA的长;
(2)∠COD的度数.
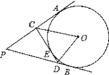
【答案】.解:(1)由切线长定理可得△PCD的周长=PA+PB,PA=PB,
∴PA=PB=6 ………………………………………(4分)
(2)连接OA、OB、OE
利用切线长定理可证∠COD=![]() ∠AOB=
∠AOB=![]() (180°-∠P)=60° ………… (8分)
(180°-∠P)=60° ………… (8分)
【解析】
(1)、可通过切线长定理将相等的线段进行转换,得出三角形PDE的周长等于PA+PB的结论,即可求出PA的长;(2)、根据三角形的内角和求出∠ADC和∠BEC的度数和,然后根据切线长定理,得出∠EDO和∠DEO的度数和,再根据三角形的内角和求出∠DOE的度数.
(1)∵CA,CE都是⊙O的切线,∴CA=CE, 同理:DE=DB,PA=PB,
∴△PCD的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,即PA的长为6;
(2)∵∠P=60°,∴∠PCE+∠PDE=120°, ∴∠ACD+∠CDB=360°-120°=240°,
∵CA,CE是⊙O的切线, ∴∠OCE=∠OCA=![]() ∠ACD; 同理:∠ODE=
∠ACD; 同理:∠ODE=![]() ∠CDB,
∠CDB,
∴∠OCE+∠ODE=![]() (∠ACD+∠CDB)=120°, ∴∠COD=180-120°=60°.
(∠ACD+∠CDB)=120°, ∴∠COD=180-120°=60°.


科目:初中数学 来源: 题型:
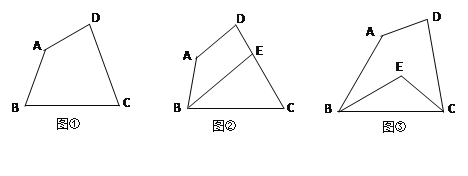
【题目】四边形ABCD中,∠A=140°,∠D=80°.
(1)如图①,若∠B=∠C,试求出∠C的度数;
(2)如图②,若∠ABC的角平分线交DC于点E,且BE∥AD,试求出∠C的度数;
(3)如图③,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点A对应的数为a,点B对应的数为b,点A在负半轴,且|a|=6,b是最小的正偶数.
(1)求线段AB的长;
(2)若点C在数轴上对应的数为x,且x是方程2x+1=3x-9的解,在数轴上是否存在点P,使得PA+PB=![]() BC+AB,若存在,求出点P对应的数,若不存在,说明理由.
BC+AB,若存在,求出点P对应的数,若不存在,说明理由.
(3)如图,若Q是B点右侧一点,QA的中点为M,N为QB的四等分点且靠近于Q点,当Q在B的右侧运动时,说明:QM﹣![]() BN的值不变,并求出其值.
BN的值不变,并求出其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今有三部自动换币机,其中甲机总是将一枚硬币换成2枚其他硬币;乙机总是将一枚硬币换成4枚其他硬币;丙机总是将一枚硬币换面10枚其他硬币.某人共进行了12次换币,便将一枚硬币换成了81枚.试问他在丙机上换了_____次?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的内切圆⊙O与AB,BC,AC分别相切于点D,E,F,若![]() ,如图①.
,如图①.
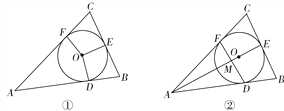
(1)判断△ABC的形状,并证明你的结论;
(2)设AE与DF相交于点M,如图②,AF=2FC=4,求AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以线段AB为直径作⊙O,CD与⊙O相切于点E,交AB的延长线于点D, 连接BE,过点O作OC∥BE交切线DE于点C,连接AC .

(1)求证:AC是⊙O的切线 ;
(2)若BD=OB=4,求弦AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证:
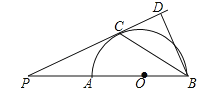
(1)∠PBC=∠CBD;
(2)![]() =ABBD.
=ABBD.
查看答案和解析>>
科目:初中数学 来源: 题型:
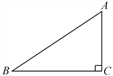
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.
(1)分别以直线AC,BC为轴,把△ABC旋转一周,得到两个不同的圆锥,求这两个圆锥的侧面积;
(2)以直线AB为轴,把△ABC旋转一周,求所得几何体的表面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用同样规格的黑、白两种颜色的正方形瓷砖按下图所示的方式铺宽为1.5米的小路.
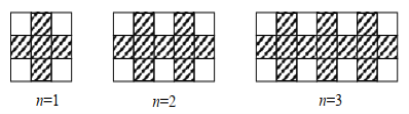
(1)铺第5个图形用黑色正方形瓷砖 块;
(2)按照此方式铺下去,铺第 n 个图形用黑色正方形瓷砖 块;(用含 n的代数式表示)
(3)若黑、白两种颜色的瓷砖规格都为( 长0.5米宽0.5米),且黑色正方形瓷砖每块价格 25 元,白色正方形瓷砖每块价格30元,若按照此方式恰好铺满该小路某一段(该段小路的总面积为 18.75 平方米),求该段小路所需瓷砖的总费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com