
【题目】已知△ABC的内切圆⊙O与AB,BC,AC分别相切于点D,E,F,若![]() ,如图①.
,如图①.
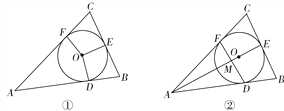
(1)判断△ABC的形状,并证明你的结论;
(2)设AE与DF相交于点M,如图②,AF=2FC=4,求AM的长.
【答案】(1)等腰三角形 (2)![]()
【解析】(1)、易证∠EOF+∠C=180°,∠DOE+∠B=180°和∠EOF=∠DOE,即可解题;(2)、连接OB、OC、OD、OF,易证AD=AF,BD=CF可得DF∥BC,再根据AE长度即可解题.
(1)等腰三角形.
证明:∵AC,AB,BC是⊙O的切线, ∴∠BDO=∠BEO=∠CFO=∠CEO=90°.
∵![]() =
=![]() ,∴∠EOF=∠EOD, ∴∠B=∠C,∴AB=AC, 即△ABC是等腰三角形;
,∴∠EOF=∠EOD, ∴∠B=∠C,∴AB=AC, 即△ABC是等腰三角形;
(2)∵AC=AB,CE=BE, ∴AE⊥BC,∠FAO=∠DAO,∵AF=AD,
∴FM=DM,AE⊥DF,∴AE过圆心O,DF∥BC,∴AF∶AC=DF∶BC,即4∶6=DF∶4,
∴DF=![]() ,∴FM=
,∴FM=![]() , ∴AM=
, ∴AM=![]() =
=![]() .
.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,O,D分别为AB,BC上的点,经过A,D两点的⊙O分别交AB,AC于点E,F,且D为弧EF的中点.
(1)求证:BC与⊙O相切;
(2)当⊙O的半径r=2,∠CAD=30°时,求劣弧AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店,甲种笔记本标价每本8元,乙种笔记本标价每本5元.今天,甲、乙两种笔记本合计卖了100本,共卖了695元!
(1)两种笔记本各销售了多少?
(2)所得销售款可能是660元吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南开两江中学校初一年级在3月18日听了一堂“树的畅想”的景观设计课,随后在本年级学生中进行了活动收获度调查,采取随机抽样的调查方式进行网络问卷调查,问卷调查的结果分为“非常有收获”“比较有收获”“收获一般”“没有太大的收获”四个等级,分别记作A、B、C、D并根据调查结果绘制两幅不完整统计图:
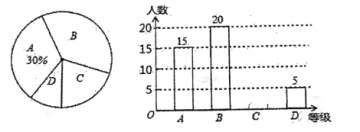
(1)这次一共调查了_______名学生,并将条形统计图补充完整
(2)请在参与调查的这些学生中,随机抽取一名学生,求抽取到的学生对这次“树的畅想”的景观设计课活动收获度是“收获一般”或者“没有太大的收获”的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
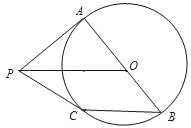
【题目】如图,AB是⊙O的直径,PA是⊙O的切线,点C在⊙O上,CB∥PO.
(1)判断PC与⊙O的位置关系,并说明理由;
(2)若AB=6,CB=4,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在数轴上有A 、B、C三个点,点A表示的数是-4,点B表示的数是-2,点C表示的数是2.
(1)在数轴上把A 、B、C三点表示出来,并比较各数的大小(用“<”连接);
(2)如何移动点B,使它到点A和点C的距离相等 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com