
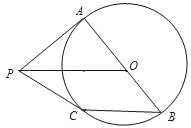
【题目】如图,AB是⊙O的直径,PA是⊙O的切线,点C在⊙O上,CB∥PO.
(1)判断PC与⊙O的位置关系,并说明理由;
(2)若AB=6,CB=4,求PC的长.
【答案】(1)PC是⊙O的切线,理由见解析;(2)![]()
【解析】试题分析:(1)要证PC是⊙O的切线,只要连接OC,再证∠PCO=90°即可.
(2)可以连接AC,根据已知先证明△ACB∽△PCO,再根据勾股定理和相似三角形的性质求出PC的长.
试题解析:(1)结论:PC是⊙O的切线.
证明:连接OC
∵CB∥PO
∴∠POA=∠B,∠POC=∠OCB
∵OC=OB
∴∠OCB=∠B
∴∠POA=∠POC
又∵OA=OC,OP=OP
∴△APO≌△CPO
∴∠OAP=∠OCP
∵PA是⊙O的切线
∴∠OAP=90°
∴∠OCP=90°
∴PC是⊙O的切线.
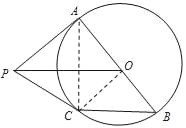
(2)连接AC
∵AB是⊙O的直径
∴∠ACB=90°(6分)
由(1)知∠PCO=90°,∠B=∠OCB=∠POC
∵∠ACB=∠PCO
∴△ACB∽△PCO
∴![]()
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】已知在△ABC中,∠ABC和∠ACB的角平分线交于O,且∠ABC的角平分线与∠ACB的外角平分线交于P,∠OPC和∠OCP角平分线交于H,∠H=117.5°,则∠A=________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的内切圆⊙O与AB,BC,AC分别相切于点D,E,F,若![]() ,如图①.
,如图①.
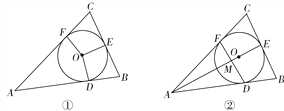
(1)判断△ABC的形状,并证明你的结论;
(2)设AE与DF相交于点M,如图②,AF=2FC=4,求AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA,PB是⊙O的切线,A,B为切点,点C在PB上,OC∥AP,CD⊥AP于点D.
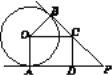
(1)求证:OC=AD;
(2)若∠P=50°,⊙O的半径为4,求四边形AOCD的周长(精确到0.1,参考数据:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证:
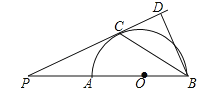
(1)∠PBC=∠CBD;
(2)![]() =ABBD.
=ABBD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是一个长方体纸盒 平面展开图,已知纸盒中相对两个面上的数互为相反数
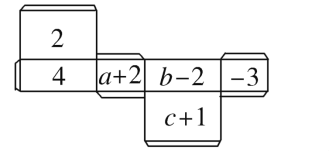
(1)填空:![]() __________,
__________,![]() ___________,
___________,![]() ___________.
___________.
(2)先化简,再求值:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线
轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线![]() ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价![]() (单位:万元)成一次函数关系.
(单位:万元)成一次函数关系.
(1)求年销售量![]() 与销售单价
与销售单价![]() 的函数关系式;
的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com