
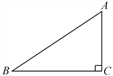
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.
(1)分别以直线AC,BC为轴,把△ABC旋转一周,得到两个不同的圆锥,求这两个圆锥的侧面积;
(2)以直线AB为轴,把△ABC旋转一周,求所得几何体的表面积.
【答案】(1) 80π;60π;(2)![]() .
.
【解析】(1)先利用勾股定理计算出AB=10,当以直线AC为轴,把△ABC旋转一周,得到的圆锥的底面半径是BC,母线长为AB,然后根据圆锥的侧面积公式计算;当以直线BC为轴,把△ABC旋转一周,得到的圆锥的底面半径为AC,母线长为AB, 然后根据圆锥的侧面积公式计算;
(2)作CD⊥AB于D,利用面积法可得到CD的长,由于以直线AB为轴,把△ABC旋转一周,所得几何体的是以CD为底面半径的两个圆锥,它的表面积就是两个圆锥的侧面积, 圆锥的侧面积公式计算.
(1)∵∠C=90°,AC=6,BC=8,
∴AB=![]() =10,
=10,
∴以直线AC为轴,把△ABC旋转一周,得到的圆锥的侧面积=π×8×10=80π;
以直线BC为轴,把△ABC旋转一周,得到的圆锥的侧面积=π×6×10=60π;
(2)如答图,过点C作CD⊥AB于点D.
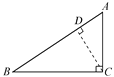
∵CD·AB=AC·BC,
∴CD=![]() =
=![]() ,
,
以直线AB为轴,把△ABC旋转一周,所得几何体是由以CD为底面半径的两个圆锥组成,则它的表面积=π×![]() ×6+π×
×6+π×![]() ×8=
×8=![]() π.
π.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
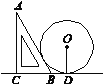
【题目】如图,一块直角三角板ABC(∠A=30°)的斜边AB与一个以r为半径的圆轮子相靠,若BD=1,则r等于( )
A. 2 B. ![]() C. 1.5 D.
C. 1.5 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个水坝的横断面,坝顶宽CD=8米,坝高DE=12米,迎水坡BC的坡比i1=1∶2,背水坡AD的坡比i2=1∶1.
求:(1)∠A的度数;
(2)坝底宽AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电力公司为鼓励市民节约用电,采取按月用电量分段收费办法,已知某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图),根据图象解下列问题:
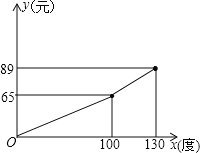
(1)写出y与x的函数关系式;
(2)利用函数关系式,说明电力公司采取的收费标准;
(3)若该用户某月用电60度,则应缴费多少元?若该用户某月缴费105元时,则该用户该月用了多少度电?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:以直线AB上一点O为端点作射线OM、ON,将一个直角三角形的直角顶点放在O处(∠COD=90°).
(1)如图1,直角三角板COD的边OD放在射线OB上,OM平分∠AOC,ON和OB重合,则∠MON=_°;
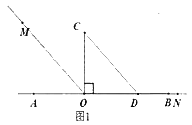
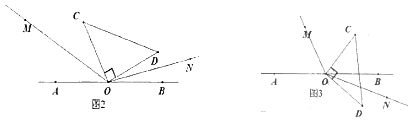
(2)直角三角板COD绕点O旋转到如图2的位置,OM平分∠AOC,ON平分∠BOD,求∠MON的度数。
(3)直角三角板COD绕点O旋转到如图3的位置,OM平分∠ AOC ,ON平分∠BOD,猜想∠MON的度数,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
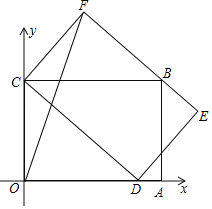
【题目】如图,矩形OABC的边OC在y轴上,边OA在x轴上,C点坐标为(0,3),点D是线段OA的一个动点,连接CD,以CD为边作矩形CDEF,使边EF过点B,已知所作矩形CDEF的面积为12,连接OF,则在点D的运动过程中,线段OF的最大值为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传节约用水,小强随机调查了某小区部分家庭3月份的用水情况,并将收集的数据整理成如下统计图.
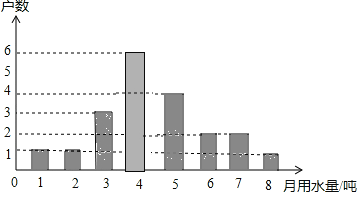
(1)小明一共调查了多少户家庭?
(2)求所调查家庭3月份用水量的众数、中位数和平均数;
(3)若该小区有800户居民,请你估计这个小区3月份的总用水量是多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com