练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图是一个水坝的横断面，坝顶宽CD＝8米，坝高DE＝12米，迎水坡BC的坡比i1＝1∶2，背水坡AD的坡比i2＝1∶1.

    求：(1)∠A的度数；

    (2)坝底宽AB.

    【答案】(1) 45°；(2)44米.

    【解析】（1）根据已知背水坡的坡度i2可求得∠A的度数；

    （2）过点C作CF⊥AB于F，从而得到DC=EF，DE=CF，再根据坡度求得BF的长，这样就不难求出AB的长．

    (1)∵tanA＝，

    ∴AE＝DE，

    ∴∠A＝45°；

    (2)如图，过点C作CF⊥AB于点F.

    ∵DE⊥AE，DC∥AB，

    ∴四边形EFCD为矩形，

    ∴DE＝CF＝12米，CD＝EF＝8米．

    ∵tanB＝，∴BF＝2CF＝24米，

    ∴AB＝AE＋EF＋BF＝12＋8＋24＝44(米)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为了测量竖直旗杆AB的高度，某综合实践小组在地面D处竖直放置标杆CD，并在地面上水平放置个平面镜E，使得B，E，D在同一水平线上，如图所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED).在F处测得旗杆顶A的仰角为39.3°，平面镜E的俯角为45°，FD=1.8米，问旗杆AB的高度约为多少米? (结果保留整数)(参考数据：tan39.3°≈0.82，tan84.3°≈10.02)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】今有三部自动换币机，其中甲机总是将一枚硬币换成2枚其他硬币；乙机总是将一枚硬币换成4枚其他硬币；丙机总是将一枚硬币换面10枚其他硬币．某人共进行了12次换币，便将一枚硬币换成了81枚．试问他在丙机上换了_____次？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，以线段AB为直径作⊙O，CD与⊙O相切于点E，交AB的延长线于点D， 连接BE，过点O作OC∥BE交切线DE于点C，连接AC ．

    （1）求证：AC是⊙O的切线 ；

    （2）若BD=OB=4，求弦AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是半圆O的直径，点P是BA延长线上一点，PC是⊙O的切线，切点为C，过点B作BD⊥PC交PC的延长线于点D，连接BC．求证：

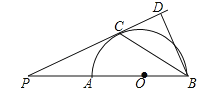
    （1）∠PBC=∠CBD；

    （2）=ABBD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，E，F，G，H分别是BD，BC，AC，AD的中点，且AB=CD，下列结论：①EG⊥FH；②四边形EFGH是菱形；③HF平分∠EHG；④EG=（BC﹣AD），其中正确的个数是（　　）

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

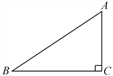
    【题目】如图，在Rt△ABC中，∠C＝90°，AC＝6，BC＝8.

    (1)分别以直线AC，BC为轴，把△ABC旋转一周，得到两个不同的圆锥，求这两个圆锥的侧面积；

    (2)以直线AB为轴，把△ABC旋转一周，求所得几何体的表面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题情境

    在综合与实践课上，老师让同学们以“两条平行线AB，CD和一块含60°角的直角三角尺EFG(∠EFG＝90°，∠EGF＝60°)”为主题开展数学活动．

    操作发现

    (1)如图(1)，小明把三角尺的60°角的顶点G放在CD上，若∠2＝2∠1，求∠1的度数；

    (2)如图(2)，小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上，请你探索并说明∠AEF与∠FGC之间的数量关系；

    结论应用

    (3)如图(3)，小亮把三角尺的直角顶点F放在CD上，30°角的顶点E落在AB上．若∠AEG＝α，则∠CFG等于______(用含α的式子表示)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料．

    在数学课上，老师请同学思考如下问题：

    已知：如图①，在△ABC中，∠A＝90°.

    图①

    求作：⊙P，使得点P在边AC上，且⊙P与AB，BC都相切．

    小轩的主要作法如下：

    如图②，

    图②

    (1)作∠ABC的平分线BF，与AC交于点P；

    (2)以P为圆心，AP长为半径作⊙P，则⊙P即为所求．

    老师说：“小轩的作法正确．”

    请回答：⊙P与BC相切的依据是 ____．

    查看答案和解析>>

    同步练习册答案