
【题目】问题情境
在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
操作发现
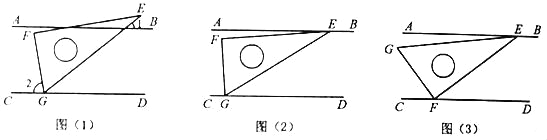
(1)如图(1),小明把三角尺的60°角的顶点G放在CD上,若∠2=2∠1,求∠1的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;
结论应用
(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,则∠CFG等于______(用含α的式子表示).

【答案】(1)∠1=40°;(2)∠AEF+∠GFC=90°;(3)60°﹣α.
【解析】
(1)依据AB∥CD,可得∠1=∠EGD,再根据∠2=2∠1,∠FGE=60°,即可得出∠EGD![]() (180°﹣60°)=40°,进而得到∠1=40°;
(180°﹣60°)=40°,进而得到∠1=40°;
(2)根据AB∥CD,可得∠AEG+∠CGE=180°,再根据∠FEG+∠EGF=90°,即可得到∠AEF+∠GFC=90°;
(3)根据AB∥CD,可得∠AEF+∠CFE=180°,再根据∠GFE=90°,∠GEF=30°,∠AEG=α,即可得到∠GFC=180°﹣90°﹣30°﹣α=60°﹣α.
(1)如图1.
∵AB∥CD,∴∠1=∠EGD.
又∵∠2=2∠1,∴∠2=2∠EGD.
又∵∠FGE=60°,∴∠EGD![]() (180°﹣60°)=40°,∴∠1=40°;
(180°﹣60°)=40°,∴∠1=40°;
(2)如图2.
∵AB∥CD,∴∠AEG+∠CGE=180°,即∠AEF+∠FEG+∠EGF+∠FGC=180°.
又∵∠FEG+∠EGF=90°,∴∠AEF+∠GFC=90°;
(3)如图3.
∵AB∥CD,∴∠AEF+∠CFE=180°,即∠AEG+∠FEG+∠EFG+∠GFC=180°.
又∵∠GFE=90°,∠GEF=30°,∠AEG=α,∴∠GFC=180°﹣90°﹣30°﹣α=60°﹣α.
故答案为:60°﹣α.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AB∥CD∥EF,BC∥AD,AC平分∠BAD,且与EF交于点O,那么与∠AOE相等的角有( )
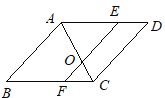
A. 6个B. 5个C. 4个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[知识生成]通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.例如:如图①是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题:
的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题:
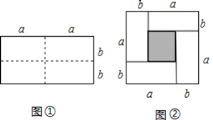
(1)图②中阴影部分的正方形的边长是________________;
(2)请用两种不同的方法求图②中阴影部分的面积:
方法1:________________________;方法2:_______________________;
(3)观察图②,请你写出![]() 、
、![]() 、
、![]() 之间的等量关系是__________;
之间的等量关系是__________;
(4)根据(3)中的等量关系解决如下问题:若![]() ,
,![]() ,则
,则![]() =________;
=________;
[知识迁移]
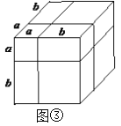
类似地,用两种不同的方法计算同一几何体的体积,也可以得到一个恒等式.
(5)根据图③,写出一个代数恒等式:____________________________;
(6)已知![]() ,
,![]() ,利用上面的规律求
,利用上面的规律求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是( )

A. 4nB. 4mC. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点O是AC的中点,AC=2AB,延长AB至G,使BG=AB,连接GO交BC于E,延长GO交AD于F,连接AE.
求证:(1)△ABC≌△AOG;
(2)猜测四边形AECF的形状并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,△ABD沿AD方向平移得△A1B1D1 , 点A1在AD边上,A1B1与BD交于点E,D1B1与CD交于点F.
(1)求证:四边形EB1FD是平行四边形;
(2)若AB=3,BC=4,AA1=1,求B1F的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=2x+4
(1)在如图所示的平面直角坐标系中,画出函数的图象;

2)求图象与x轴的交点A的坐标,与y轴交点B的坐标;
(3)在(2)的条件下,求出△AOB的面积;
(4)利用图象直接写出:当y<0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() ,OB、OC、OM、ON是
,OB、OC、OM、ON是![]() 内的射线.
内的射线.
![]() 如图1,若OM平分
如图1,若OM平分![]() ,ON平分
,ON平分![]() 当OB绕点O在
当OB绕点O在![]() 内旋转时,则
内旋转时,则![]() 的大小为______;
的大小为______;
![]() 如图2,若
如图2,若![]() ,OM平分
,OM平分![]() ,ON平分
,ON平分![]() 当
当![]() 绕点O在
绕点O在![]() 内旋转时,求
内旋转时,求![]() 的大小;
的大小;
![]() 在
在![]() 的条件下,若
的条件下,若![]() ,当
,当![]() 在
在![]() 内绕着点O以
内绕着点O以![]() 秒的速度逆时针旋转t秒时,
秒的速度逆时针旋转t秒时,![]() 和
和![]() 中的一个角的度数恰好是另一个角的度数的两倍,求t的值
中的一个角的度数恰好是另一个角的度数的两倍,求t的值

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com