
【题目】如图,四边形ABCD是矩形,△ABD沿AD方向平移得△A1B1D1 , 点A1在AD边上,A1B1与BD交于点E,D1B1与CD交于点F.
(1)求证:四边形EB1FD是平行四边形;
(2)若AB=3,BC=4,AA1=1,求B1F的长.
【答案】
(1)证明:∵△A1B1D1是由△ABD平移所得,
∴AB∥A1B1,BD∥B1D1,
∵四边形ABCD是矩形,
∴AB∥CD,
∴A1B1∥CD,
∴四边形EB1FD是平行四边形.
(2)解:∵四边形ABCD是矩形,
∴∠A=90°,AB=CD=3,AD=BC=4,
∴BD= ![]() =5,
=5,
∵AA1=BB1=1,
∴CB1=3,
∵FB1∥BD,
∴△CB1F∽△CBD,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴B1F= ![]() .
.
【解析】(1)要证四边形EB1FD是平行四边形,只要证明两组对边分别平行即可;(2)由△CB1F∽△CBD,得![]() ,由此即可解决问题.
,由此即可解决问题.
【考点精析】解答此题的关键在于理解平行四边形的判定与性质的相关知识,掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P点作PF⊥AD交BC的延长线于点F,交AC于点H.(1)∠APB的度数为_______°;(2)求证:△ABP≌△FBP;(3)求证:AH+BD=AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校“百变魔方”社团准备购买![]() ,
,![]() 两种魔方.已知购买2个
两种魔方.已知购买2个![]() 种魔方和6个
种魔方和6个![]() 种魔方共需130元,购买3个
种魔方共需130元,购买3个![]() 种魔方和4个
种魔方和4个![]() 种魔方所需款数相同.
种魔方所需款数相同.
(1)求这两种魔方的单价;
(2)结合社员们的需求,社团决定购买![]() ,
,![]() 两种魔方共100个(其中
两种魔方共100个(其中![]() 种魔方不超过50个).某商店有两种优惠活动,如图所示.
种魔方不超过50个).某商店有两种优惠活动,如图所示.
请根据以上信息,说明选择哪种优惠活动购买魔方更实惠.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境
在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
操作发现
(1)如图(1),小明把三角尺的60°角的顶点G放在CD上,若∠2=2∠1,求∠1的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;
结论应用
(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,则∠CFG等于______(用含α的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
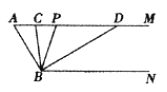
【题目】如图,已知AM//BN,∠A=600.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)①∠ABN的度数是 ;②∵AM //BN,∴∠ACB=∠ ;
(2)求∠CBD的度数;
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(4)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于不等式组 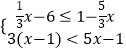 ,下列说法正确的是( )
,下列说法正确的是( )
A.此不等式组的正整数解为1,2,3
B.此不等式组的解集为﹣1<x≤ ![]()
C.此不等式组有5个整数解
D.此不等式组无解
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为原点,已知数轴上点A和点B所表示的数分别为![]() 和8,动点M从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时动点N从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.
和8,动点M从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时动点N从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.
![]() 当
当![]() 时,
时,![]() ______个单位长度,
______个单位长度,![]() ______个单位长度,此时MN的中点C所对应的有理数为______;
______个单位长度,此时MN的中点C所对应的有理数为______;
![]() 在运动过程中,当
在运动过程中,当![]() 时,求点M所对应的有理数.
时,求点M所对应的有理数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列各题:
(1)x取何值时,代数式3x+2的值不大于代数式4x+3的值?
(2)当m为何值时,关于x的方程![]() x-1=m的解不小于3?
x-1=m的解不小于3?
(3)已知不等式2(x+3)-4<0, 化简:︳4x+1︱-︱2-4x︱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1:y=2x+1、直线l2:y=﹣x+7,直线l1、l2分别交x轴于B、C两点,l1、l2相交于点A.
(1)求A、B、C三点坐标;
(2)求△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com