
【题目】如图,在Rt△ABC中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P点作PF⊥AD交BC的延长线于点F,交AC于点H.(1)∠APB的度数为_______°;(2)求证:△ABP≌△FBP;(3)求证:AH+BD=AB.

【答案】(1)135°,(2)见解析,(3)见解析
【解析】
(1)根据角平分线性质可得∠PAB+∠PBA=45°,即可解题.
(2)易得∠DPB=45°,可得∠BPF=135°,即可证得△ABP≌△FBP;
(3)由(2)可知∠F=∠BAD,AP=PF,AB=BF,即可求得∠F=∠CAD,可得AH=DF,即可解题.
(1)∵AD平分∠BAC,BE平分∠ABC,
∴∠PAB+∠PBA=![]() (∠ABC+∠BAC)=45°,
(∠ABC+∠BAC)=45°,
∴∠APB=180°-45°=135°.
(2)∵∠APB=135°.
∴∠DPB=45°,
∵PF⊥AD,
∴∠BPF=135°,
在△ABP和△FBP中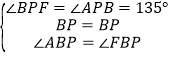
∴△ABP≌△FBP(ASA)
(3)∵△ABP≌△FBP,
∴∠F=∠BAD,AP=PF,AB=BF,
∵∠BAD=∠CAD,
∴∠F=∠CAD,
在△APH和△FPD中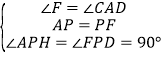
∴△APH≌△FPD(ASA)
∴AH=DF,
∵BF=DF+BD
∴AB=AH+BD


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是BC的中点,CE⊥AD,垂足为点E,BF∥AC交CE的延长线于点F.
求证:AC=2BF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,每个小立方体的棱长为1,图1中共有1个立方体,其中1个看得见,0个看不见;图2中共有8个小立方体,其中7个看得见,1个看不见;图3中共有27个小立方体,其中19个看得见,8个看不见;……;则第10个图形中,其中看得见的小立方体个数是( )
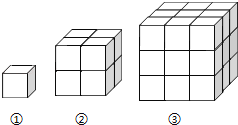
A. 270 B. 271 C. 272 D. 273
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O是正方形ABCD对角线BD的中点.
(1)如图1,若点E是OD的中点,点F是AB上一点,且使得∠CEF=90°,过点E作ME∥AD,交AB于点M,交CD于点N.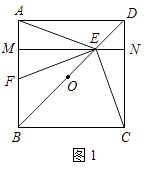
①∠AEM=∠FEM; ②点F是AB的中点;
(2)如图2,若点E是OD上一点,点F是AB上一点,且使 ![]() =
= ![]() =
= ![]() ,请判断△EFC的形状,并说明理由;
,请判断△EFC的形状,并说明理由;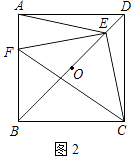
(3)如图3,若E是OD上的动点(不与O,D重合),连接CE,过E点作EF⊥CE,交AB于点F,当 ![]() =
= ![]() 时,请猜想
时,请猜想 ![]() 的值(请直接写出结论).
的值(请直接写出结论).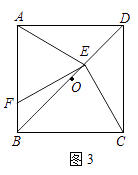
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我市的空气质量情况,某环保兴趣小组从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).

请你根据图中提供的信息,解答下列问题:
(1)请补全条形统计图,并求扇形统计图中表示“重度污染”的扇形的圆心角度数;
(2)所抽取若干天的空气质量情况的众数是 中位数是 .
(3)请估计该市这一年(365天)达到“优”和“良”的总天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
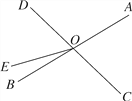
【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.
(1)图中∠AOC的对顶角为________,∠BOE的补角为________;
(2)若∠AOC=75°,且∠BOE∶∠EOD=1∶4,求∠AOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD∥EF,BC∥AD,AC平分∠BAD,且与EF交于点O,那么与∠AOE相等的角有( )
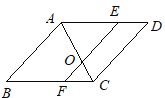
A. 6个B. 5个C. 4个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,△ABD沿AD方向平移得△A1B1D1 , 点A1在AD边上,A1B1与BD交于点E,D1B1与CD交于点F.
(1)求证:四边形EB1FD是平行四边形;
(2)若AB=3,BC=4,AA1=1,求B1F的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com