
【题目】如图,点O为原点,已知数轴上点A和点B所表示的数分别为![]() 和8,动点M从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时动点N从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.
和8,动点M从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时动点N从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.
![]() 当
当![]() 时,
时,![]() ______个单位长度,
______个单位长度,![]() ______个单位长度,此时MN的中点C所对应的有理数为______;
______个单位长度,此时MN的中点C所对应的有理数为______;
![]() 在运动过程中,当
在运动过程中,当![]() 时,求点M所对应的有理数.
时,求点M所对应的有理数.
![]()
【答案】(1)6,4,![]() ;(2)
;(2)![]() 时,M对应数字是3或
时,M对应数字是3或![]() .
.
【解析】
(1)AM=3t,BN=2t,表示出M,N所表示的数字,二者和的一半即中点C对应数字;
(2)分M在右边,N在左边和M在左边,N在右边两种可能.用t表示MN的长度,根据MN![]() AB列方程求解.
AB列方程求解.
(1)M从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,点N从点B出发,以每秒2个单位长度的速度沿数轴向左匀速运动,t秒后,AM=3t,MN=2t,当t=2时,AM=6,BN=4,此时M、N对应数字是﹣6和4,所以MN![]() .
.
故答案为:6,4,﹣1;
(2)M、N对应数字是﹣12+3t和8﹣2t.
当M在左边,N在右边时,MN=8﹣2t﹣(﹣12+3t)=20﹣5t.
∵MN![]() AB,∴20﹣5t
AB,∴20﹣5t![]() ,∴t=3,所以此时M对应数字是﹣3;
,∴t=3,所以此时M对应数字是﹣3;
当M在右边,N在左边时,MN=﹣12+3t﹣(8﹣2t)=﹣20+5t.
∵MN![]() AB,∴﹣20+5t
AB,∴﹣20+5t![]() ,∴t=5,所以此时M对应数字是3.
,∴t=5,所以此时M对应数字是3.
综上所述:当MN![]() AB时,M对应数字是3或﹣3.
AB时,M对应数字是3或﹣3.


科目:初中数学 来源: 题型:
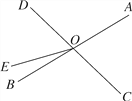
【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.
(1)图中∠AOC的对顶角为________,∠BOE的补角为________;
(2)若∠AOC=75°,且∠BOE∶∠EOD=1∶4,求∠AOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是( )

A. 4nB. 4mC. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,△ABD沿AD方向平移得△A1B1D1 , 点A1在AD边上,A1B1与BD交于点E,D1B1与CD交于点F.
(1)求证:四边形EB1FD是平行四边形;
(2)若AB=3,BC=4,AA1=1,求B1F的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+b与反比例函数y= ![]() (x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(1)求m的值;
(2)求直线AB的解析式;
(3)若直线x=t(t>1)与直线y=kx+b交于点M,与x轴交于点N,连接AN,S△AMN= ![]() ,求t的值.
,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=2x+4
(1)在如图所示的平面直角坐标系中,画出函数的图象;

2)求图象与x轴的交点A的坐标,与y轴交点B的坐标;
(3)在(2)的条件下,求出△AOB的面积;
(4)利用图象直接写出:当y<0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O在直线MN上,∠AOB=90°,OC平分∠MOB.
(1)若∠AOC=![]() 则∠BOC=_______,∠AOM=_______,∠BON=_________;
则∠BOC=_______,∠AOM=_______,∠BON=_________;
(2)若∠AOC=![]() 则∠BON=_______(用含有
则∠BON=_______(用含有![]() 的式子表示);
的式子表示);
(3)将∠AOB绕着点O顺时针转到图2的位置,其他条件不变,若∠AOC=![]() (
(![]() 为钝角),求∠BON的度数(用含
为钝角),求∠BON的度数(用含![]() 的式子表示).
的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小强和小华共同站在路灯下,小强的身高EF=1.8m,小华的身高MN=1.5m,他们的影子恰巧等于自己的身高,即BF=1.8m,CN=1.5m,且两人相距4.7m,则路灯AD的高度是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣x+2分别与x轴,y轴交于A,B两点,与双曲线y= ![]() 交于E,F两点,若AB=2EF,则k的值是( )
交于E,F两点,若AB=2EF,则k的值是( )
A.﹣1
B.1
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com