
【题目】如图1,点O在直线MN上,∠AOB=90°,OC平分∠MOB.
(1)若∠AOC=![]() 则∠BOC=_______,∠AOM=_______,∠BON=_________;
则∠BOC=_______,∠AOM=_______,∠BON=_________;
(2)若∠AOC=![]() 则∠BON=_______(用含有
则∠BON=_______(用含有![]() 的式子表示);
的式子表示);
(3)将∠AOB绕着点O顺时针转到图2的位置,其他条件不变,若∠AOC=![]() (
(![]() 为钝角),求∠BON的度数(用含
为钝角),求∠BON的度数(用含![]() 的式子表示).
的式子表示).

【答案】(1)59°40′; 29°20′; 60°40′; (2)2α;
(3)360°-2α.
【解析】
(1)根据∠BOC=∠AOB-∠AOC进行计算即可,
由OC平分∠MOB得∠BOM=2∠BOC,则∠AOM=∠BOM-∠AOB,
∠BON=180°-∠BOM,代入计算即可得出答案;
(2)仿照(1)中方法,先求出∠BOC,再求得∠BOM,最后再代入∠BON=180°-∠BOM化简即可;
(3)由图可知∠BOC=∠AOC-∠AOB,然后由角平分线定义得∠BOM=2∠BOC,最后代入∠BON=180°-∠BOM化简即可得出答案.
解:(1)∠BOC=∠AOB-∠AOC
=90°-30°20′
=59°40′,
∵OC平分∠MOB,
∴∠BOM=2∠BOC=2×59°40′=119°20′,
∴∠AOM=∠BOM-∠AOB
=119°20′-90°
=29°20′,
∠BON=180°-∠BOM
=180°-119°20′
=60°40′.
故答案为:59°40′,29°20′,60°40′;
(2)∠BOC=∠AOB-∠AOC=90°-α,
∵OC平分∠MOB,
∴∠BOM=2∠BOC=2(90°-α)=180°-2α,
∴∠BON=180°-∠BOM
=180°-(180°-2α)
=2α.
故答案为:2α;
(3)由图可知∠BOC=∠AOC-∠AOB=α-90°,
∵OC平分∠MOB,
∴∠BOM=2∠BOC=2(α-90°)= 2α-180°,
∴∠BON=180°-∠BOM
=180°-(2α-180°)
=360°-2α.


科目:初中数学 来源: 题型:
【题目】如图,某学生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD= ![]() .
. 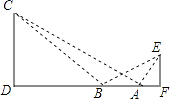
(1)求旗杆EF的高(结果保留根号);
(2)求旗杆EF与实验楼CD之间的水平距离DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于 . 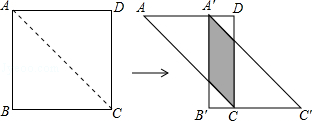
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级(1)班的宣传委员在办黑板报时,采用了下面的图案作为边框,其中每个黑色六边形与6个自色六边形相邻,若一段边框上有25个黑色六边形,则这段边框共有白色六边形

A. 100个 B. 102个 C. 98个 D. 150个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,Rt△ABC绕点A顺时针旋转到Rt△ADE的位置,点E在斜边AB上,连结BD,过点D作DF⊥AC于点F.
(1)如图1,若点F与点A重合,求证:AC=BC;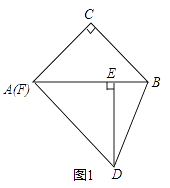
(2)若∠DAF=∠DBA,
①如图2,当点F在线段CA的延长线上时,判断线段AF与线段BE的数量关系,并说明理由;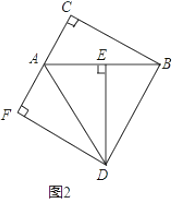
②当点F在线段CA上时,设BE=x,请用含x的代数式表示线段AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】希望中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制的不完整的统计图,则下列说法中,不正确的是( )
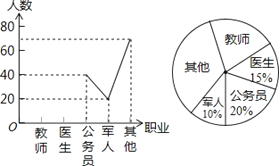
A. 被调查的学生有200人
B. 被调查的学生中喜欢教师职业的有40人
C. 被调查的学生中喜欢其他职业的占40%
D. 扇形图中,公务员部分所对应的圆心角为72°
查看答案和解析>>
科目:初中数学 来源: 题型:
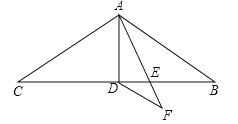
【题目】如图在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=_______度;
(2)如图2如果∠BAC=60°,则∠BCE=______度;
(3)设∠BAC=![]() ,∠BCE=
,∠BCE=![]() .
.
①如图3,当点D在线段BC上移动,则![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,请直接写出![]() 之样的数量关系,不用证明。
之样的数量关系,不用证明。




查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com