
【题目】在Rt△ABC中,∠C=90°,Rt△ABC绕点A顺时针旋转到Rt△ADE的位置,点E在斜边AB上,连结BD,过点D作DF⊥AC于点F.
(1)如图1,若点F与点A重合,求证:AC=BC;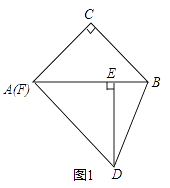
(2)若∠DAF=∠DBA,
①如图2,当点F在线段CA的延长线上时,判断线段AF与线段BE的数量关系,并说明理由;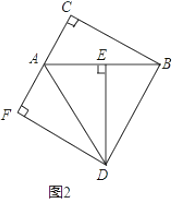
②当点F在线段CA上时,设BE=x,请用含x的代数式表示线段AF.
【答案】
(1)
解:由旋转得,∠BAC=∠BAD,
∵DF⊥AC,
∴∠CAD=90°,
∴∠BAC=∠BAD=45°,
∵∠ACB=90°,
∴∠ABC=45°,
∴AC=CB
(2)
解:①由旋转得,AD=AB,
∴∠ABD=∠ADB,
∵∠DAF=∠ABD,
∴∠DAF=∠ADB,
∴AF∥BD,
∴∠BAC=∠ABD,
∵∠ABD=∠FAD
由旋转得,∠BAC=∠BAD,
∴∠FAD=∠BAC=∠BAD= ![]() ×180°=60°,
×180°=60°,
由旋转得,AB=AD,
∴△ABD是等边三角形,
∴AD=BD,
在△AFD和△BED中,
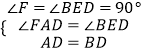 ,
,
∴△AFD≌△BED,
∴AF=BE,
②如图,

由旋转得,∠BAC=∠BAD,
∵∠ABD=∠FAD=∠BAC+∠BAD=2∠BAD,
由旋转得,AD=AB,
∴∠ABD=∠ADB=2∠BAD,
∵∠BAD+∠ABD+∠ADB=180°,
∴∠BAD+2∠BAD+2∠BAD=180°,
∴∠BAD=36°,
设BD=y,作BG平分∠ABD,
∴∠BAD=∠GBD=36°
∴AG=BG=BD=y,
∴DG=AD﹣AG=AD﹣BG=AD﹣BD,
∵∠BDG=∠ADB,
∴△BDG∽△ADB,
∴ ![]() .
.
∴ ![]() =
= ![]() ﹣1,即(
﹣1,即( ![]() )2﹣
)2﹣ ![]() ﹣1=0,
﹣1=0,
∴ ![]() ,
,
∵∠FAD=∠EBD,∠AFD=∠BED,
∴△AFD∽△BED,
∴ ![]() ,
,
∴AF= ![]() =
= ![]() x
x
【解析】(1)由旋转得到∠BAC=∠BAD,而DF⊥AC,从而得出∠ABC=45°,最后判断出△ABC是等腰直角三角形;(2)①由旋转得到∠BAC=∠BAD,再根据∠DAF=∠DBA,从而求出∠FAD=∠BAC=∠BAD=60°,最后判定△AFD≌△BED,即可;②根据题意画出图形,先求出角度,得到△ABD是顶角为36°的等腰三角形,再用相似求出, ![]() ,最后判断出△AFD∽△BED,代入即可.
,最后判断出△AFD∽△BED,代入即可.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F. 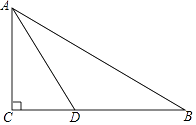
(1)用尺规补全图形(保留作图痕迹,不写作法);
(2)求证:BC与⊙O相切;
(3)当AD= ![]() ,∠CAD=30°时,求劣弧AD的长.
,∠CAD=30°时,求劣弧AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时血液中含药量最高,达到每毫升6微克,接着就逐步衰减,10小时后血液中含药量为每毫升3微克,每毫升血液中含药量![]() (微克)随时间
(微克)随时间![]() (小时)的变化如图所示,那么成年人规定剂量服药后:
(小时)的变化如图所示,那么成年人规定剂量服药后:
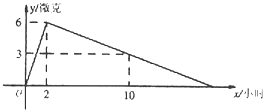
(1)y与x之间的函数关系式.
(2)如果每毫升血液中含药量在4微克或4微克以上时,治疗疾病才是有效的,那么这个有效时
间是多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O在直线MN上,∠AOB=90°,OC平分∠MOB.
(1)若∠AOC=![]() 则∠BOC=_______,∠AOM=_______,∠BON=_________;
则∠BOC=_______,∠AOM=_______,∠BON=_________;
(2)若∠AOC=![]() 则∠BON=_______(用含有
则∠BON=_______(用含有![]() 的式子表示);
的式子表示);
(3)将∠AOB绕着点O顺时针转到图2的位置,其他条件不变,若∠AOC=![]() (
(![]() 为钝角),求∠BON的度数(用含
为钝角),求∠BON的度数(用含![]() 的式子表示).
的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点A(﹣1,2),B(2,﹣3)在直线y=kx+b上,则函数y= ![]() 的图象在( )
的图象在( )
A.第一、三象限
B.第一、二象限
C.第二、四象限
D.第二、三象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,AD=9,AB=6,若点G、H、M、N分别在AB、CD、AD、BC上,线段MN与GH交于点K.若∠GKM=45°,NM=3 ![]() ,则GH= .
,则GH= . 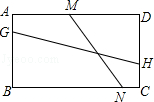
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com