
【题目】如图,已知矩形ABCD,AD=9,AB=6,若点G、H、M、N分别在AB、CD、AD、BC上,线段MN与GH交于点K.若∠GKM=45°,NM=3 ![]() ,则GH= .
,则GH= . 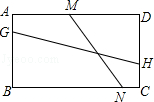
【答案】3 ![]()
【解析】解:如图,过点A作AE∥GH交CD于E,作AF∥MN交BC于F, 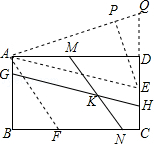
则AF=MN=3 ![]() ,AE=GH,
,AE=GH,
∵∠GKM=45°,
∴∠BAF+∠DAE=90°﹣45°=45°,
作∠QAE=45°交CD的延长线于Q,
则∠QAD+∠DAE=45°,
∴∠QAD=∠FAB,
∵∠B=∠ADQ=90°,
∴△ABF∽△AQD,
∴ ![]() ,
,
∴ ![]() ,
,
∴AQ= ![]() ,
,
在Rt△ADQ中,DQ= ![]() =
= ![]() ,
,
过点E作EP⊥AQ于P,
∵∠QAE=45°,
∴△AEP是等腰直角三角形,
设GH=AE=x,则AP=EP= ![]() AE=
AE= ![]() x,
x,
∵tan∠Q= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得x=3 ![]() ,
,
所以GH=3 ![]() .
.
故答案为:3 ![]() .
.
过点A作AE∥GH交CD于E,作AF∥MN交BC于F,于是得到AF=MN=3 ![]() ,AE=GH,由于∠GKM=45°,得到∠BAF+∠DAE=90°﹣45°=45°,作∠QAE=45°交CD的延长线于Q,推出∠QAD+∠DAE=45°,通过△ABF≌△AQD,根据相似三角形的性质得到
,AE=GH,由于∠GKM=45°,得到∠BAF+∠DAE=90°﹣45°=45°,作∠QAE=45°交CD的延长线于Q,推出∠QAD+∠DAE=45°,通过△ABF≌△AQD,根据相似三角形的性质得到 ![]() ,求得AQ=
,求得AQ= ![]() ,在Rt△ADQ中,由勾股定理得到DQ=
,在Rt△ADQ中,由勾股定理得到DQ= ![]() =
= ![]() ,过点E作EP⊥AQ于P,得到△AEP是等腰直角三角形,设GH=AE=x,则AP=EP=
,过点E作EP⊥AQ于P,得到△AEP是等腰直角三角形,设GH=AE=x,则AP=EP= ![]() AE=
AE= ![]() ,然后利用∠Q的正切值列出方程求解即可.
,然后利用∠Q的正切值列出方程求解即可.


科目:初中数学 来源: 题型:
【题目】如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于 . 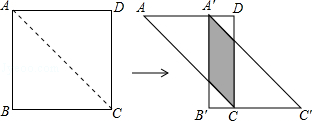
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,Rt△ABC绕点A顺时针旋转到Rt△ADE的位置,点E在斜边AB上,连结BD,过点D作DF⊥AC于点F.
(1)如图1,若点F与点A重合,求证:AC=BC;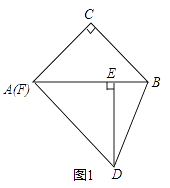
(2)若∠DAF=∠DBA,
①如图2,当点F在线段CA的延长线上时,判断线段AF与线段BE的数量关系,并说明理由;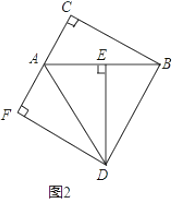
②当点F在线段CA上时,设BE=x,请用含x的代数式表示线段AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】希望中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制的不完整的统计图,则下列说法中,不正确的是( )
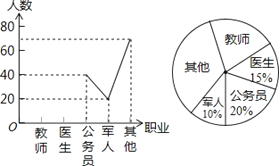
A. 被调查的学生有200人
B. 被调查的学生中喜欢教师职业的有40人
C. 被调查的学生中喜欢其他职业的占40%
D. 扇形图中,公务员部分所对应的圆心角为72°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,求DF的长.
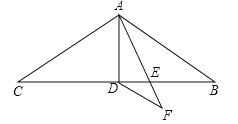
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将一副直角三角板的顶点叠合在一起,记为点O(∠C=30°,∠A=45°).
(1)当∠AOC=45°时,求∠DOB的度数;
(2)请探究∠AOC和∠DOB之间满足的数量关系,并说明理由.
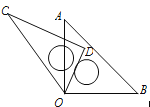
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村计划对总长为1800m的道路进行改造,安排甲、乙两个工程队完成![]() 已知甲队每天能完成的道路长度是乙队每天能完成的2倍,并且在独立完成长为400m的道路时,甲队比乙队少用4天.
已知甲队每天能完成的道路长度是乙队每天能完成的2倍,并且在独立完成长为400m的道路时,甲队比乙队少用4天.
![]() 求甲、乙两工程队每天能完成道路的长度分别是多少m?
求甲、乙两工程队每天能完成道路的长度分别是多少m?
![]() 若村委每天需付给甲队的道路改造费用为
若村委每天需付给甲队的道路改造费用为![]() 万元,乙队为
万元,乙队为![]() 万元,要使这次的道路改造费用不超过8万元,至少应安排甲队工作多少天?
万元,要使这次的道路改造费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com