
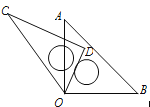
【题目】如图所示,将一副直角三角板的顶点叠合在一起,记为点O(∠C=30°,∠A=45°).
(1)当∠AOC=45°时,求∠DOB的度数;
(2)请探究∠AOC和∠DOB之间满足的数量关系,并说明理由.
【答案】(1)∠DOB=75°(2)∠DOB-∠AOC=30°,理由见解析.
【解析】
(1)根据三角板的各角度数,明确∠COD=60°,∠AOC=45°,表示出∠DOB= ∠AOB-∠AOD即可解题;(2)由∠AOB永远比∠COD大30°可知,当两个角减掉相同角度后,关系仍成立即可解题.
解:(1)解: 因为∠COD=60°,∠AOC=45°
所以∠AOD= ∠COD-∠AOC=15°
因为∠AOB=90°
所以∠DOB= ∠AOB-∠AOD=75°
(2)解:因为∠COD=60°
所以∠AOD= ∠COD-∠AOC=60°-∠AOC
因为∠AOB=90°
所以∠DOB= ∠AOB-∠AOD=90°-(60°- ∠AOC)=30°+∠AOC
即∠DOB-∠AOC=30°


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F. 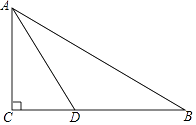
(1)用尺规补全图形(保留作图痕迹,不写作法);
(2)求证:BC与⊙O相切;
(3)当AD= ![]() ,∠CAD=30°时,求劣弧AD的长.
,∠CAD=30°时,求劣弧AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,AD=9,AB=6,若点G、H、M、N分别在AB、CD、AD、BC上,线段MN与GH交于点K.若∠GKM=45°,NM=3 ![]() ,则GH= .
,则GH= . 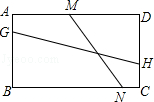
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与理解: 图1是边长分别为a和b(a>b)的两个等边三角形纸片ABC和C′DE叠放在一起(C与C′重合)的图形.
操作与证明:
(1)操作:固定△ABC,将△C′DE绕点C按顺时针方向旋转30°,连接AD,BE,如图2;在图2中,线段BE与AD之间具有怎样的大小关系?证明你的结论; 
(2)操作:若将图1中的△C′DE,绕点C按顺时针方向任意旋转一个角度α,连接AD,BE,如图3;在图3中,线段BE与AD之间具有怎样的大小关系?证明你的结论; 
猜想与发现:
根据上面的操作过程,请你猜想当α为多少度时,线段AD的长度最大是多少?当α为多少度时,线段AD的长度最小是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,三角形ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(2,4),点B的坐标为(1,1),点C的坐标为(3,2).
(1)将三角形ABC先沿着x轴负方向平移6个单位,再沿y轴负方向平移2个单位得到三角形A1B1C1,在图中画出三角形A1B1C1;
(2)分别写出A1,B1、C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】花粉的质量很小,一粒某种植物花粉的质量约为0.000037毫克,已知1克=1000毫克,那么0.000037毫克可用科学记数法表示为
A. 3.7×10﹣5克 B. 3.7×10﹣6克 C. 37×10﹣7克 D. 3.7×10﹣8克
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com