
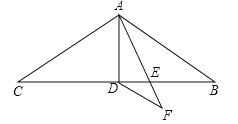
【题目】如图在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,求DF的长.
【答案】4.5.
【解析】
试题分析:由等腰三角形三线合一的性质可得AD⊥BC,∠BAD=∠CAD,再求出∠DAE=∠EAB=30°,然后由平行线的性质求出∠F=∠BAE=30°,从而得到∠DAE=∠F,再由等角对等边求出AD=DF,然后求出∠B=30°,由直角三角形30°角所对的直角边等于斜边的一半解答.
试题解析:解:∵AB=AC,AD是△ABC的中线,∴AD⊥BC,∠BAD=∠CAD=![]() ∠BAC=
∠BAC=![]() ×120°=60°,∵AE是∠BAD的角平分线,∴∠DAE=∠EAB=
×120°=60°,∵AE是∠BAD的角平分线,∴∠DAE=∠EAB=![]() ∠BAD=
∠BAD=![]() ×60°=30°,∵DF∥AB,∴∠F=∠BAE=30°,∴∠DAE=∠F=30°,∴AD=DF,∵∠B=90°﹣60°=30°,∴AD=
×60°=30°,∵DF∥AB,∴∠F=∠BAE=30°,∴∠DAE=∠F=30°,∴AD=DF,∵∠B=90°﹣60°=30°,∴AD=![]() AB=
AB=![]() ×9=4.5,∴DF=4.5.
×9=4.5,∴DF=4.5.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() :
:![]() 交
交![]() 、
、![]() 轴分别为
轴分别为![]() 、
、![]() 两点,
两点,![]() 点与
点与![]() 点关于
点关于![]() 轴对称.动点
轴对称.动点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上(点
上(点![]() 不与点
不与点![]() 、
、![]() 重合),满足
重合),满足![]() .
.
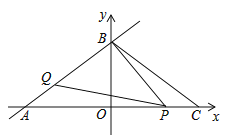
(1)点![]() 坐标是 ,
坐标是 ,![]() .
.
(2)当点![]() 在什么位置时,
在什么位置时,![]() ,说明理由.
,说明理由.
(3)当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O在直线MN上,∠AOB=90°,OC平分∠MOB.
(1)若∠AOC=![]() 则∠BOC=_______,∠AOM=_______,∠BON=_________;
则∠BOC=_______,∠AOM=_______,∠BON=_________;
(2)若∠AOC=![]() 则∠BON=_______(用含有
则∠BON=_______(用含有![]() 的式子表示);
的式子表示);
(3)将∠AOB绕着点O顺时针转到图2的位置,其他条件不变,若∠AOC=![]() (
(![]() 为钝角),求∠BON的度数(用含
为钝角),求∠BON的度数(用含![]() 的式子表示).
的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,AD=9,AB=6,若点G、H、M、N分别在AB、CD、AD、BC上,线段MN与GH交于点K.若∠GKM=45°,NM=3 ![]() ,则GH= .
,则GH= . 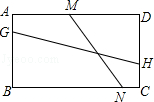
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解2017年八年级学生课外书籍借阅情况.从中随机抽取了40名学生进行调查,根据调查结果列出如下的表格,并绘制成如图所示的扇形统计图,其中科普类本数占这40名学生借阅总本数的40%.

(1)求表格中字母m的值及扇形统计图中“教辅类”所对应的圆心角α的度数;
(2)该校2017年八年级有500名学生,请你估计该年级学生共借阅教辅类书籍约多少本.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与理解: 图1是边长分别为a和b(a>b)的两个等边三角形纸片ABC和C′DE叠放在一起(C与C′重合)的图形.
操作与证明:
(1)操作:固定△ABC,将△C′DE绕点C按顺时针方向旋转30°,连接AD,BE,如图2;在图2中,线段BE与AD之间具有怎样的大小关系?证明你的结论; 
(2)操作:若将图1中的△C′DE,绕点C按顺时针方向任意旋转一个角度α,连接AD,BE,如图3;在图3中,线段BE与AD之间具有怎样的大小关系?证明你的结论; 
猜想与发现:
根据上面的操作过程,请你猜想当α为多少度时,线段AD的长度最大是多少?当α为多少度时,线段AD的长度最小是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线EF与AB交于点M,与CD交于点O,OG平分∠DOF,若∠COM=120°,∠EMB=![]() ∠COF.
∠COF.

(1)求∠FOG的度数;
(2)写出一个与∠FOG互为同位角的角;
(3)求∠AMO的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com