
【题目】如图,直线![]() :
:![]() 交
交![]() 、
、![]() 轴分别为
轴分别为![]() 、
、![]() 两点,
两点,![]() 点与
点与![]() 点关于
点关于![]() 轴对称.动点
轴对称.动点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上(点
上(点![]() 不与点
不与点![]() 、
、![]() 重合),满足
重合),满足![]() .
.
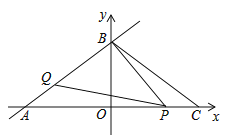
(1)点![]() 坐标是 ,
坐标是 ,![]() .
.
(2)当点![]() 在什么位置时,
在什么位置时,![]() ,说明理由.
,说明理由.
(3)当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,10;(2)当
,10;(2)当![]() 的坐标是
的坐标是![]() 时,
时,![]() ;(3)当
;(3)当![]() 为等腰三角形时,点
为等腰三角形时,点![]() 的坐标是
的坐标是![]() 或
或![]() .
.
【解析】
(1)把x=0和y=0分别代入一次函数的解析式,求出A、B的坐标,根据勾股定理求出BC即可;
(2)求出∠PAQ=∠BCP,∠AQP=∠BPC,根据点的坐标求出AP=BC,根据全等三角形的判定推出即可;
(3)分为三种情况:①PQ=BP,②BQ=QP,③BQ=BP,根据(2)即可推出①,根据三角形外角性质即可判断②,根据勾股定理得出方程,即可求出③.
解:(1)∵![]() ,∴当
,∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,即
,即![]() 的坐标是
的坐标是![]() ,
,![]() 的坐标是
的坐标是![]() ,∵
,∵![]() 点与
点与![]() 点关于
点关于![]() 轴对称,∴
轴对称,∴![]() 的坐标是
的坐标是![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,
,
由勾股定理得:![]() ,故答案为:
,故答案为:![]() ,10.
,10.
(2)当![]() 的坐标是
的坐标是![]() 时,
时,![]() ,理由是:∵
,理由是:∵![]() ,
,![]() ,∴
,∴![]() ,∵
,∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() 和
和![]() 关于
关于![]() 轴对称,∴
轴对称,∴![]() ,
,
在![]() 和
和![]() 中,
中,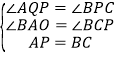 ,∴
,∴![]() ,∴当
,∴当![]() 的坐标是
的坐标是![]() 时,
时,![]() .
.
(3)分为三种情况:
①当![]() 时,∵由(2)知,
时,∵由(2)知,![]() ,∴
,∴![]() ,即此时
,即此时![]() 的坐标是
的坐标是![]() ;
;
②当![]() 时,则
时,则![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
而根据三角形的外角性质得:![]() ,∴此种情况不存在;
,∴此种情况不存在;
③当![]() 时,则
时,则![]() ,即
,即![]() ,设此时
,设此时![]() 的坐标是
的坐标是![]() ,
,
∵在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,∴
,∴![]() ,解得:
,解得:![]() ,
,
即此时![]() 的坐标是
的坐标是![]() .∴当
.∴当![]() 为等腰三角形时,点
为等腰三角形时,点![]() 的坐标是
的坐标是![]() 或
或![]() .
.
故答案为:(1)![]() ,10;(2)当
,10;(2)当![]() 的坐标是
的坐标是![]() 时,
时,![]() ;(3)当
;(3)当![]() 为等腰三角形时,点
为等腰三角形时,点![]() 的坐标是
的坐标是![]() 或
或![]() .
.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
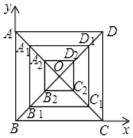
【题目】如图以正方形ABCD的B点为坐标原点.BC所在直线为x轴,BA所在直线为y轴,建立直角坐标系.设正方形ABCD的边长为6,顺次连接OA、OB、OC、OD的中点A1、B1、C1、D1,得到正方形A1B1C1D1,再顺次连接OA1、OB1、OC1、OD1的中点得到正方形A2B2C2D2.按以上方法依次得到正方形A1B1C1D1,……AnBnCnDn,(n为不小于1的自然数),设An点的坐标为(xn,yn),则xn+yn=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
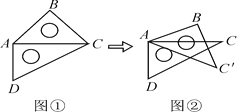
【题目】取一副三角板按图①拼接,固定三角板ADC,将三角板ABC绕点A按顺时针方向旋转得到△ABC′,如图②所示.设∠CAC′=α(0°<α≤45°).
(1)当α=15°时,求证:AB∥CD;
(2)连接BD,当0°<α≤45°时,∠DBC′+∠CAC′+∠BDC的度数是否变化,若变化 ,求出变化范围;若不变,求出其度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连结AB、AE、BE.已知tan∠CBE= ![]() ,A(3,0),D(﹣1,0),E(0,3).
,A(3,0),D(﹣1,0),E(0,3).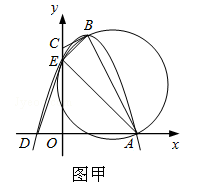
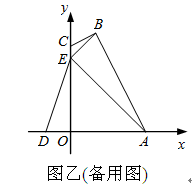
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
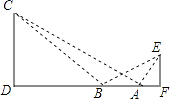
【题目】如图,某学生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD= ![]() .
. 
(1)求旗杆EF的高(结果保留根号);
(2)求旗杆EF与实验楼CD之间的水平距离DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于 . 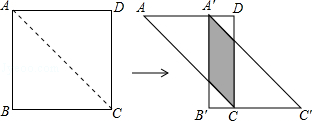
查看答案和解析>>
科目:初中数学 来源: 题型:
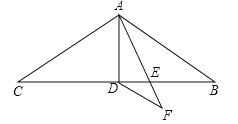
【题目】如图在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,求DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com