
【题目】如图,某学生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD= ![]() .
. 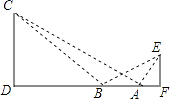
(1)求旗杆EF的高(结果保留根号);
(2)求旗杆EF与实验楼CD之间的水平距离DF的长.
【答案】
(1)解:∵∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD= ![]() ,
,
∴tan60°= ![]() ,tan30°=
,tan30°= ![]() ,
,
解得,EF=5 ![]() ,AF=5,
,AF=5,
即旗杆EF的高为5 ![]() 米
米
(2)解:∵∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD= ![]() ,AF=5,
,AF=5,
∴CD=BD, ![]() ,
,
设CD=3a,则BD=3a,AD=4a,
∴AB=a=10,
∴BD=3a=30,
∴DF=AD+AF=40+5=45,
即旗杆EF与实验楼CD之间的水平距离DF的长是45米
【解析】(1)根据题目中的数据和锐角三角函数可以求得EF和AF的长,从而可以解答本题;(2)根据题目中的数据和锐角三角函数可以求得AD和AF的长,从而可以得到旗杆EF与实验楼CD之间的水平距离DF的长.


科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P,Q分别是边OB,OA上的动点,记∠OPM=α,∠OQN=β,当MP+PQ+QN最小时,则关于α,β的数量关系正确的是( )

A. β﹣α=60° B. β+α=210° C. β﹣2α=30° D. β+2α=240°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,填空:
(1)若∠4=∠3,则____∥_____,理由是______;
(2)若∠2=∠E,则____∥___,理由是____;
(3)若∠A=∠ABE=180°,则____∥___,理由是____;
(4)若∠2=∠____,则DA∥EB,理由是____;
(5)若∠DBC+∠_____=180°,则DB∥EC,理由是____;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() :
:![]() 交
交![]() 、
、![]() 轴分别为
轴分别为![]() 、
、![]() 两点,
两点,![]() 点与
点与![]() 点关于
点关于![]() 轴对称.动点
轴对称.动点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上(点
上(点![]() 不与点
不与点![]() 、
、![]() 重合),满足
重合),满足![]() .
.
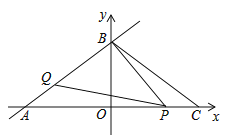
(1)点![]() 坐标是 ,
坐标是 ,![]() .
.
(2)当点![]() 在什么位置时,
在什么位置时,![]() ,说明理由.
,说明理由.
(3)当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为表彰在某活动中表现积极的同学,老师决定购买文具盒与钢笔作为奖品.已知5个文具盒、2支钢笔共需100元;3个文具盒、1支钢笔共需57元.
(1)每个文具盒、每支钢笔各多少元?
(2)若本次表彰活动,老师决定购买10件作为奖品,若购买![]() 个文具盒,10件奖品共需
个文具盒,10件奖品共需![]() 元,求
元,求![]() 与
与![]() 的函数关系式.如果至少需要购买3个文具盒,本次活动老师最多需要花多少钱?
的函数关系式.如果至少需要购买3个文具盒,本次活动老师最多需要花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F. 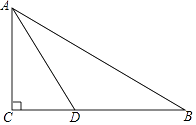
(1)用尺规补全图形(保留作图痕迹,不写作法);
(2)求证:BC与⊙O相切;
(3)当AD= ![]() ,∠CAD=30°时,求劣弧AD的长.
,∠CAD=30°时,求劣弧AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
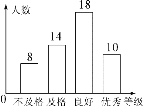
【题目】我校进行“宪法知识”宣传培训后进行了一次测试.学生考分按标准划分为不合格、合格、良好、优秀四个等级,为了解全校的考试情况,对在校的学生随机抽样调查,得到如图所示的条形统计图,请结合统计图回答下列问题:
(1)该校抽样调查的学生人数为________人,抽样中考生分数的中位数所在等级是________;
(2)抽样中不及格的人数是多少?占被调查人数的百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O在直线MN上,∠AOB=90°,OC平分∠MOB.
(1)若∠AOC=![]() 则∠BOC=_______,∠AOM=_______,∠BON=_________;
则∠BOC=_______,∠AOM=_______,∠BON=_________;
(2)若∠AOC=![]() 则∠BON=_______(用含有
则∠BON=_______(用含有![]() 的式子表示);
的式子表示);
(3)将∠AOB绕着点O顺时针转到图2的位置,其他条件不变,若∠AOC=![]() (
(![]() 为钝角),求∠BON的度数(用含
为钝角),求∠BON的度数(用含![]() 的式子表示).
的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与理解: 图1是边长分别为a和b(a>b)的两个等边三角形纸片ABC和C′DE叠放在一起(C与C′重合)的图形.
操作与证明:
(1)操作:固定△ABC,将△C′DE绕点C按顺时针方向旋转30°,连接AD,BE,如图2;在图2中,线段BE与AD之间具有怎样的大小关系?证明你的结论; 
(2)操作:若将图1中的△C′DE,绕点C按顺时针方向任意旋转一个角度α,连接AD,BE,如图3;在图3中,线段BE与AD之间具有怎样的大小关系?证明你的结论; 
猜想与发现:
根据上面的操作过程,请你猜想当α为多少度时,线段AD的长度最大是多少?当α为多少度时,线段AD的长度最小是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com