
【题目】如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P,Q分别是边OB,OA上的动点,记∠OPM=α,∠OQN=β,当MP+PQ+QN最小时,则关于α,β的数量关系正确的是( )

A. β﹣α=60° B. β+α=210° C. β﹣2α=30° D. β+2α=240°
【答案】B
【解析】
如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP+PQ+QN最小易知∠OPM=∠OPM′=∠NPQ,∠OQP=∠AQN′=∠AQN,KD∠OQN=180°-30°-∠ONQ,∠OPM=∠NPQ=30°+∠OQP,∠OQP=∠AQN=30°+∠ONQ,由此即可解决问题.
如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP+PQ+QN最小,
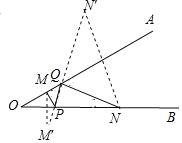
易知∠OPM=∠OPM′=∠NPQ,∠OQP=∠AQN′=∠AQN,
∵∠OQN=180°-30°-∠ONQ,∠OPM=∠NPQ=30°+∠OQP,∠OQP=∠AQN=30°+∠ONQ,
∴α+β=180°-30°-∠ONQ+30°+30°+∠ONQ=210°.
故选B.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的条件是( )
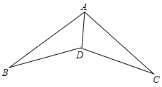
A. ∠B=∠C,BD=DC B. ∠ADB=∠ADC,BD=DC
C. ∠B=∠C,∠BAD=∠CAD D. BD=DC,AB=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图以正方形ABCD的B点为坐标原点.BC所在直线为x轴,BA所在直线为y轴,建立直角坐标系.设正方形ABCD的边长为6,顺次连接OA、OB、OC、OD的中点A1、B1、C1、D1,得到正方形A1B1C1D1,再顺次连接OA1、OB1、OC1、OD1的中点得到正方形A2B2C2D2.按以上方法依次得到正方形A1B1C1D1,……AnBnCnDn,(n为不小于1的自然数),设An点的坐标为(xn,yn),则xn+yn=______.
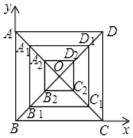
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
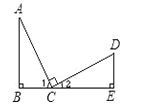
A. ∠1=∠2 B. ∠A =∠2 C. △ABC≌△CED D. ∠A与∠D互为余角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某学生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动10米到B处,测得∠EBF=30°,∠CBD=45°,tan∠CAD= ![]() .
. 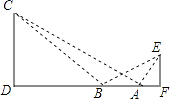
(1)求旗杆EF的高(结果保留根号);
(2)求旗杆EF与实验楼CD之间的水平距离DF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com