
【题目】阅读下面材料.
在数学课上,老师请同学思考如下问题:
已知:如图①,在△ABC中,∠A=90°.

图①
求作:⊙P,使得点P在边AC上,且⊙P与AB,BC都相切.
小轩的主要作法如下:
如图②,

图②
(1)作∠ABC的平分线BF,与AC交于点P;
(2)以P为圆心,AP长为半径作⊙P,则⊙P即为所求.
老师说:“小轩的作法正确.”
请回答:⊙P与BC相切的依据是 ____.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图是一个水坝的横断面,坝顶宽CD=8米,坝高DE=12米,迎水坡BC的坡比i1=1∶2,背水坡AD的坡比i2=1∶1.
求:(1)∠A的度数;
(2)坝底宽AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的边OC在y轴上,边OA在x轴上,C点坐标为(0,3),点D是线段OA的一个动点,连接CD,以CD为边作矩形CDEF,使边EF过点B,已知所作矩形CDEF的面积为12,连接OF,则在点D的运动过程中,线段OF的最大值为__.
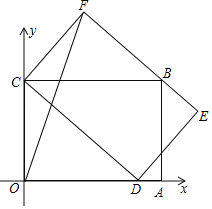
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解全校学生对电视节目的喜爱情况(新闻、体育、动画、娱乐、戏曲),从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.

请根据以上信息,解答下列问题:
(1)这次被调查的学生共有多少人?
(2)请将条形统计图补充完整;
(3)若该校约有1500名学生,估计全校学生中喜欢娱乐节目的有多少人?
(4)该校广播站需要广播员,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】再读教材:
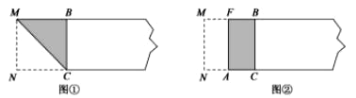
宽与长的比是 ![]() (约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
(约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.
第二步,如图②.把这个正方形折成两个相等的矩形,再把纸片展平.
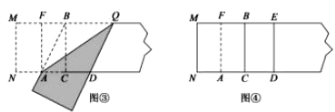
第三步,折出内侧矩形的对角线 AB,并把 AB折到图③中所示的AD处,
第四步,展平纸片,按照所得的点D折出 DE,使 DE⊥ND,则图④中就会出现黄金矩形,
问题解决:
(1)图③中AB=________(保留根号);
(2)如图③,判断四边形 BADQ的形状,并说明理由;
(3)请写出图④中所有的黄金矩形,并选择其中一个说明理由.
(4)结合图④.请在矩形 BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在x轴和y轴上,OC=3,OA=![]() ,D是BC的中点,将△OCD沿直线OD折叠后得到△OGD,延长OG交AB于点E,连接DE,则点G的坐标为 .
,D是BC的中点,将△OCD沿直线OD折叠后得到△OGD,延长OG交AB于点E,连接DE,则点G的坐标为 .
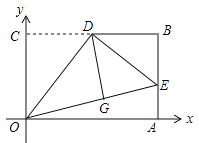
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传节约用水,小强随机调查了某小区部分家庭3月份的用水情况,并将收集的数据整理成如下统计图.
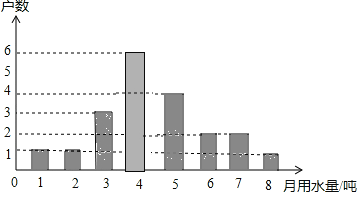
(1)小明一共调查了多少户家庭?
(2)求所调查家庭3月份用水量的众数、中位数和平均数;
(3)若该小区有800户居民,请你估计这个小区3月份的总用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一个三角形,分别连接这个三角形三边的中点得到图②,再分别连接图②中间的小三角形三边的中点,得到图③.

(1)图②有__________个三角形;图③有________个三角形;
(2)按上面的方法继续下去,第10个图有_________个三角形,第![]() 个图形中有_______个三角形.(用含
个图形中有_______个三角形.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
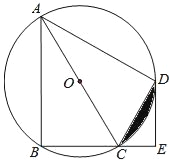
【题目】如图,四边形ABCD是⊙O的内接四边形,![]() ,AC为直径,DE⊥BC,垂足为E.
,AC为直径,DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)若AC=9,CE=3,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com