
【题目】用同样规格的黑、白两种颜色的正方形瓷砖按下图所示的方式铺宽为1.5米的小路.
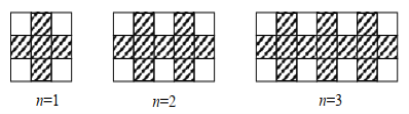
(1)铺第5个图形用黑色正方形瓷砖 块;
(2)按照此方式铺下去,铺第 n 个图形用黑色正方形瓷砖 块;(用含 n的代数式表示)
(3)若黑、白两种颜色的瓷砖规格都为( 长0.5米宽0.5米),且黑色正方形瓷砖每块价格 25 元,白色正方形瓷砖每块价格30元,若按照此方式恰好铺满该小路某一段(该段小路的总面积为 18.75 平方米),求该段小路所需瓷砖的总费用.
【答案】(1)21;(2)4n+1;(3)2005元.
【解析】
(1)根据题意构造出第五个图形的形状,数黑色正方形瓷砖的块数,即可得出答案;
(2)多画几个图形,总结规律,即可得出答案;
(3)分别求出黑白两种瓷砖的块数,乘以各自的价格即可得出答案.
解:(1)由题意可得,铺第5个图形用黑色正方形瓷砖21块;
(2)铺第1个图形用黑色正方形瓷砖5块
铺第2个图形用黑色正方形瓷砖9=5+4块
铺第3个图形用黑色正方形瓷砖13=5+4+4块
铺第4个图形用黑色正方形瓷砖17=5+4+4+4块
铺第5个图形用黑色正方形瓷砖21=5+4+4+4+4块
……
∴铺第n个图形用黑色正方形瓷砖5+4(n-1)=4n+1块
故答案为:4n+1.
(3)18.75÷(0.5×0.5)=75(块)
由题意可得,铺第n个图形共用正方形瓷砖9+6(n-1)=6n+3块,铺第n个图形用白色正方形瓷砖4+2(n-1)=2n+2块
6n+3=75,解得:n=12
可知,第12个图形用黑色正方形:4×12+1=49块,用白色正方形:2×12+2=26块
所以总费用=49×25+26×30=2005(元)
答:该段小路所需瓷砖的总费用为2005元.


科目:初中数学 来源: 题型:
【题目】如图1,已知矩形ABED,点C是边DE的中点,且AB=2AD.
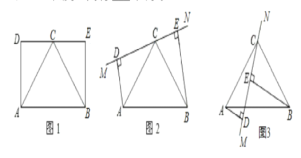
(1)由图1通过观察、猜想可以得到线段AC与线段BC的数量关系为___,位置关系为__;
(2)保持图1中的△ABC固定不变,绕点C旋转DE所在的直线MN到图2中的位置(当垂线AD、BE在直线MN的同侧).试探究线段AD、BE、DE长度之间有什么关系?并给予证明(第一问中得到的猜想结论可以直接在证明中使用);
(3)保持图2中的△ABC固定不变,继续绕点C旋转DE所在的直线MN到图3中的位置(当垂线段AD、BE在直线MN的异侧).试探究线段AD、BE、DE长度之间有___关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教育行政部门为了解该市九年级学生上学期参加综合实践活动的情况,随机调查了该市光明中学九年级学生上学期参加综合实践活动的时间,并用得到的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息,回答下列问题:
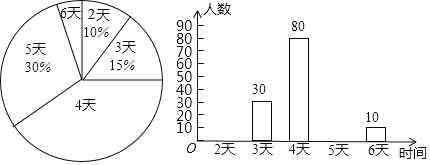
(1)试求出该校九年级学生总数;
(2)分别求出活动时间为2天、5天的学生人数,并补全条形统计图;
(3)如果该市九年级学生共约50000人,请你估计“活动时间不少于4天”的有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级二班的几位同学正在一起讨论一个关于数轴上的点表示数的题目:
甲说:“这条数轴上的两个点![]() 、
、![]() 表示的数都是绝对值是4的数”;
表示的数都是绝对值是4的数”;
乙说:“点![]() 表示负整数,点
表示负整数,点![]() 表示正整数,且这两个数的差是3”;
表示正整数,且这两个数的差是3”;
丙说:“点![]() 表示的数的相反数是它本身”.
表示的数的相反数是它本身”.
(1)请你根据以上三位同学的发言,画出一条数轴,并描出![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个不同的点.
五个不同的点.
(2)求这个五个点表示的数的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级一班和二班各推选![]() 名同学进行投篮比赛,按照比赛规则,每人各投了
名同学进行投篮比赛,按照比赛规则,每人各投了![]() 个球,两个班选手的进球数统计如下表,请根据表中数据回答问题.
个球,两个班选手的进球数统计如下表,请根据表中数据回答问题.
进球数(个) |
|
|
|
|
|
|
一班人数(人) |
|
|
|
|
|
|
二班人数(人) |
|
|
|
|
|
|
![]() 填表;
填表;
平均数 | 中位数 | 众数 | 方差 | |
一班 | 2.6 | |||
二班 | 7 | 7 | 7 |
![]() 如果要从这两个班中选出一个班代表级部参加学校的投篮比赛,争取夺得总进球数团体第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?
如果要从这两个班中选出一个班代表级部参加学校的投篮比赛,争取夺得总进球数团体第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某小学“演讲大赛”选拔赛初赛中,甲、乙、丙三位评委对小选手的综合表现,分别给出“待定”(用字母W表示)或“通过”(用字母P表示)的结论.
⑴请用树状图表示出三位评委给小选手琪琪的所有可能的结论;
⑵对于小选手琪琪,只有甲、乙两位评委给出相同结论的概率是多少?
⑶比赛规定,三位评委中至少有两位给出“通过”的结论,则小选手可入围进入复赛,问琪琪进入复赛的概率是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
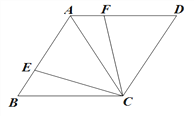
【题目】如图,四边形ABCD中,∠B=60°,对角线AC=BC,点E在AB上,将CE绕点C顺时针旋转60得CF,且点F在AD上.
(1)求证:AF=BE;
(2)若AE=DF,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,A点坐标为(-2,2).
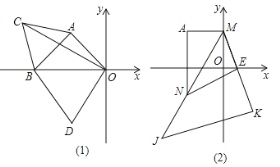
⑴如图⑴,在△ABO为等腰直角三角形,求B点坐标.
⑵如图⑴,在⑴的条件下,分别以AB和OB为边作等边△ABC和等边△OBD,连结OC,求∠COB的度数.
⑶如图⑵,过点A作AM⊥y轴于点M,点E为x轴正半轴上一点,K为ME延长线上一点,以MK为直角边作等腰直角三角形MKJ,∠MKJ=90°,过点A作AN⊥x轴交MJ于点N,连结EN.则①![]() 的值不变;②
的值不变;②![]() 的值不变,其中有且只有一个结论正确,请判断出正确的结论,并加以证明和求出其值.
的值不变,其中有且只有一个结论正确,请判断出正确的结论,并加以证明和求出其值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com