
【题目】如图所示,在平面直角坐标系中,A点坐标为(-2,2).
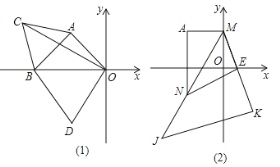
⑴如图⑴,在△ABO为等腰直角三角形,求B点坐标.
⑵如图⑴,在⑴的条件下,分别以AB和OB为边作等边△ABC和等边△OBD,连结OC,求∠COB的度数.
⑶如图⑵,过点A作AM⊥y轴于点M,点E为x轴正半轴上一点,K为ME延长线上一点,以MK为直角边作等腰直角三角形MKJ,∠MKJ=90°,过点A作AN⊥x轴交MJ于点N,连结EN.则①![]() 的值不变;②
的值不变;②![]() 的值不变,其中有且只有一个结论正确,请判断出正确的结论,并加以证明和求出其值.
的值不变,其中有且只有一个结论正确,请判断出正确的结论,并加以证明和求出其值.
【答案】(1)B(4,0);(2)30°;(3)![]() =1;
=1;
【解析】
(1)作AE⊥OB于点E,由点A的坐标就可以求出OE的值,就可以求出OB的值而得出结论.
(2)由等腰直角三角形和等边三角形的性质就可以得出∠CAO的值,再由等腰三角形的性质就可以求出∠AOC的值,从而得出结论;
(3)在AN上取一点P,使AP=OE,证明△APM≌△OEM,就可以得出MP=ME,∠AMP=∠OME,由等腰直角三角形的性质就可以得出∠PMN=∠EMN,得出△PMN≌△EMN就可以得出结论.
(1)如图1,作AE⊥OB于点E,
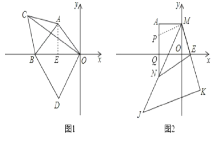
∴∠AEO=90°.
∵A(2,2).
∴OE=AE=2.
∵AB=AO,
∴BO=2EO=4.
∴B(4,0);
(2)∵△ABO为等腰直角三角形,
∴AB=AO,∠BAO=90°,∠AOB=45°.
∵△ABC是等边三角形,
∴∠BAC=60°,AC=AB,
∴∠CAO=150°,AC=AO,
∴∠ACO=∠AOC=15°,
∴∠COB=45°15°=30°;
(3) ![]() 的值不变
的值不变
理由:如图2,在AN上取一点P,使AP=OE,
∵AM⊥y轴,AN⊥x轴,
∴∠AQO=∠AMO=90°.
∵∠MOQ=90°,
∴四边形AMOQ是矩形。
∵A(2,2),
∴AQ=OQ=2,
∴四边形AMOQ是正方形,
∴∠A=∠MOE=∠AMO=90°,
AM=OM.
在△APM和△OEM中,
 ,
,
∴△APM≌△OEM(SAS),
∴MP=ME,∠AMP=∠OME.
∵∠AMP+∠PMO=90°,
∴∠OME+∠PMO=90°,
即∠PME=90°.
∵△MKJ等腰直角三角形,
∴∠JMK=45°,
∴∠PMN=45°,
∴∠PMN=∠EMN.
在△PMN和△EMN中,
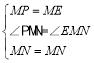 ,
,
∴△PMN≌△EMN(SAS),
∴PN=EN.
∵PN=ANAP,
∴PN=AN0E,
∴ANOE=EN.
∴![]() =1
=1


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】用同样规格的黑、白两种颜色的正方形瓷砖按下图所示的方式铺宽为1.5米的小路.
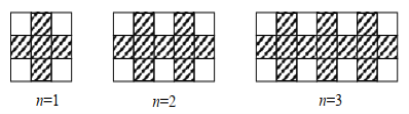
(1)铺第5个图形用黑色正方形瓷砖 块;
(2)按照此方式铺下去,铺第 n 个图形用黑色正方形瓷砖 块;(用含 n的代数式表示)
(3)若黑、白两种颜色的瓷砖规格都为( 长0.5米宽0.5米),且黑色正方形瓷砖每块价格 25 元,白色正方形瓷砖每块价格30元,若按照此方式恰好铺满该小路某一段(该段小路的总面积为 18.75 平方米),求该段小路所需瓷砖的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲船从![]() 码头出发顺流驶向
码头出发顺流驶向![]() 码头,同时乙船从
码头,同时乙船从![]() 码头出发逆流驶向
码头出发逆流驶向![]() 码头,甲,乙两船到达
码头,甲,乙两船到达![]() ,
,![]() 两码头后立即返回,乙船返回后行驶20千米与返回的甲船相遇,甲,乙两船在静水中的平均速度不变,
两码头后立即返回,乙船返回后行驶20千米与返回的甲船相遇,甲,乙两船在静水中的平均速度不变,![]() ,
,![]() 两码头间的水流速度为4千米/时,甲船逆流而行的速度与乙船顺流而行的速度相等,甲船顺流而行速度是乙船逆流而行速度的2倍,则
两码头间的水流速度为4千米/时,甲船逆流而行的速度与乙船顺流而行的速度相等,甲船顺流而行速度是乙船逆流而行速度的2倍,则![]() ,
,![]() 两码头间的路程为_______千米.
两码头间的路程为_______千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() ,
,![]() ,试说明
,试说明![]() .
.
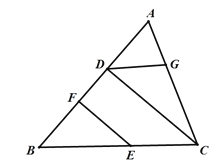
将下面的解答过程补充完整,并填空(理由或数学式)
解:∵![]() ,
,![]() (_______________),
(_______________),
∴![]() ______(______________________),
______(______________________),
∴![]() _________(____________________)
_________(____________________)
又∵![]() (已知),
(已知),
∴![]() ________(_____________________),
________(_____________________),
∴![]() _______(_____________________),
_______(_____________________),
∴![]() (_____________________)
(_____________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
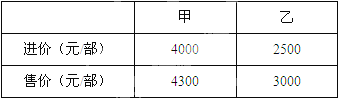
该商场计划购进两种手机若干部,共需15.5万元,预计全部销售后可获毛利润共2.1万元.
(毛利润=(售价﹣进价)×销售量)
(1)该商场计划购进甲、乙两种手机各多少部?
(2) 通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为了开展乒乓球比赛活动,准备购买一些乒乓球和乒乓球拍,通过去商店了解情况,甲乙两家商店出售同样品牌的乒乓球和乒乓球拍,乒乓球拍每副定价48元,乒乓球每盒定价12元,经商谈,甲乙两家商店给出了如下优惠措施:甲店每买一副乒乓球拍赠送一盒乒乓球,乙店全部按定价的9折优惠.现该班急需乒乓球拍5副,乒乓球![]() 盒(不少于5盒).
盒(不少于5盒).
(1)请用含![]() 的代数式分别表示去甲、乙两店购买所需的费用;
的代数式分别表示去甲、乙两店购买所需的费用;
(2)当需要购买40盒乒乓球时,通过计算,说明此时去哪家商店购买较为合算;
(3)当需要购买40盒乒乓球时,你能给出一种更为省钱的方法吗?试写出你的购买方法和所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“单词的记忆效率”是指复习一定量的单词,一周后能正确默写出的单词个数与复习的单词个数的比值.右图描述了某次单词复习中![]() 四位同学的单词记忆效率
四位同学的单词记忆效率![]() 与复习的单词个数
与复习的单词个数![]() 的情况,则这四位同学在这次单词复习中正确默写出的单词个数最多的是( )
的情况,则这四位同学在这次单词复习中正确默写出的单词个数最多的是( )
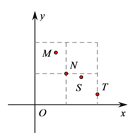
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,老师给出了如下问题:

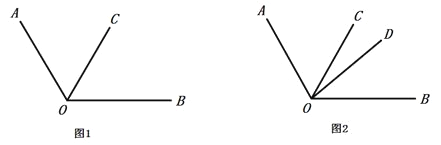
(1)以下是小刚的解答过程,请你将解答过程补充完整:
解:如图2,因为![]() ,
,![]() 平分
平分![]() ,
,
所以![]() ______
______![]() ______
______![]() (角平分线的定义).
(角平分线的定义).
因为![]() ,
,
所以![]() ______
______![]() .
.
(2)小戴说:“我觉得这道题有两种情况,小刚考虑的是![]() 在
在![]() 内部的情况,事实上,
内部的情况,事实上,![]() 还可能在
还可能在![]() 的内部”.根据小戴的想法,请你在图1中画出另一种情况对应的图形,并直接写出
的内部”.根据小戴的想法,请你在图1中画出另一种情况对应的图形,并直接写出![]() 的度数:______.
的度数:______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com