
【题目】甲船从![]() 码头出发顺流驶向
码头出发顺流驶向![]() 码头,同时乙船从
码头,同时乙船从![]() 码头出发逆流驶向
码头出发逆流驶向![]() 码头,甲,乙两船到达
码头,甲,乙两船到达![]() ,
,![]() 两码头后立即返回,乙船返回后行驶20千米与返回的甲船相遇,甲,乙两船在静水中的平均速度不变,
两码头后立即返回,乙船返回后行驶20千米与返回的甲船相遇,甲,乙两船在静水中的平均速度不变,![]() ,
,![]() 两码头间的水流速度为4千米/时,甲船逆流而行的速度与乙船顺流而行的速度相等,甲船顺流而行速度是乙船逆流而行速度的2倍,则
两码头间的水流速度为4千米/时,甲船逆流而行的速度与乙船顺流而行的速度相等,甲船顺流而行速度是乙船逆流而行速度的2倍,则![]() ,
,![]() 两码头间的路程为_______千米.
两码头间的路程为_______千米.
 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】某市教育行政部门为了解该市九年级学生上学期参加综合实践活动的情况,随机调查了该市光明中学九年级学生上学期参加综合实践活动的时间,并用得到的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息,回答下列问题:
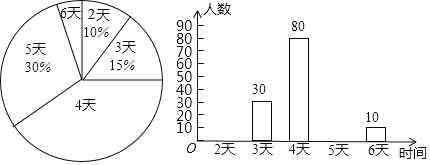
(1)试求出该校九年级学生总数;
(2)分别求出活动时间为2天、5天的学生人数,并补全条形统计图;
(3)如果该市九年级学生共约50000人,请你估计“活动时间不少于4天”的有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
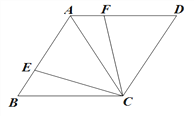
【题目】如图,四边形ABCD中,∠B=60°,对角线AC=BC,点E在AB上,将CE绕点C顺时针旋转60得CF,且点F在AD上.
(1)求证:AF=BE;
(2)若AE=DF,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知过点B(1,0)的直线![]() 与直线
与直线![]() :
:![]() 相交于点P(-1,a).且l1与y轴相交于C点,l2与x轴相交于A点.
相交于点P(-1,a).且l1与y轴相交于C点,l2与x轴相交于A点.
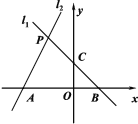
(1)求直线![]() 的解析式;
的解析式;
(2)求四边形![]() 的面积;
的面积;
(3)若点Q是x轴上一动点,连接PQ、CQ,当△QPC周长最小时,求点Q坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
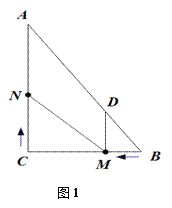
【题目】如图1,在Rt△ABC中,∠C=90,BC=6,AC=8.动点M从点B开始沿边BC向点C以每秒1个单位长度的速度运动,动点N从点C开始沿边CA向点A以每秒2个单位长度的速度运动,点M、N同时出发,且当其中一点到达端点时,另一点也随之停止运动.过点M作MD∥AC,交AB于点D,连接MN.设运动时间为t秒(t≥0).
(1)当t为何值时,四边形ADMN为平行四边形?
(2)是否存在t的值,使四边形ADMN为菱形?若存在,求出t的值;若不存在,说明理由.并探究只改变点N的速度(匀速运动),使四边形ADMN在某一时刻为菱形,求点N的速度;
(3)如图2,在整个运动过程中,求出线段MN中点P所经过的路径长.
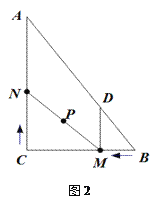
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,EF与AB,CD分别交于点G,H,∠CHG的平分线HM交AB于点M,若∠EGB=50°,则∠GMH的度数为( )
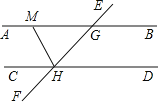
A. 50°B. 55°C. 60°D. 65°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,A点坐标为(-2,2).
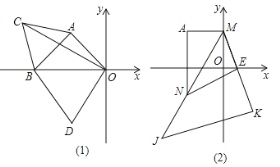
⑴如图⑴,在△ABO为等腰直角三角形,求B点坐标.
⑵如图⑴,在⑴的条件下,分别以AB和OB为边作等边△ABC和等边△OBD,连结OC,求∠COB的度数.
⑶如图⑵,过点A作AM⊥y轴于点M,点E为x轴正半轴上一点,K为ME延长线上一点,以MK为直角边作等腰直角三角形MKJ,∠MKJ=90°,过点A作AN⊥x轴交MJ于点N,连结EN.则①![]() 的值不变;②
的值不变;②![]() 的值不变,其中有且只有一个结论正确,请判断出正确的结论,并加以证明和求出其值.
的值不变,其中有且只有一个结论正确,请判断出正确的结论,并加以证明和求出其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】简单多面体是各个面都是多边形组成的几何体,十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)和棱数(E)之间存在一个有趣的关系式,称为欧拉公式.如表是根据左边的多面体模型列出的不完整的表:
多面体 | 顶点数 | 面数 | 棱数 |
四面体 | 4 | 4 | 6 |
长方体 | 8 | 6 | |
正八面体 | 8 | 12 |
现在有一个多面体,它的每一个面都是三角形,它的面数(F)和棱数(E)的和为30,则这个多面体的顶点数V=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com