
【题目】已知,如图,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() ,
,![]() ,试说明
,试说明![]() .
.
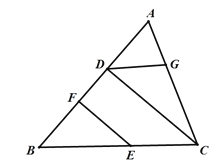
将下面的解答过程补充完整,并填空(理由或数学式)
解:∵![]() ,
,![]() (_______________),
(_______________),
∴![]() ______(______________________),
______(______________________),
∴![]() _________(____________________)
_________(____________________)
又∵![]() (已知),
(已知),
∴![]() ________(_____________________),
________(_____________________),
∴![]() _______(_____________________),
_______(_____________________),
∴![]() (_____________________)
(_____________________)
【答案】已知;在同一平面内,垂直于同一条直线的两条直线平行;∠BCD(两直线平行,同位角相等);DG(同旁内角互补,两直线平行);∠BCD(两直线平行,内错角相等);∠CDG(等量代换).
【解析】
根据垂直定义和平行线的判定推出EF∥CD,推出∠BEF=∠BCD,根据平行线的判定推出BC∥DG,根据平行线的性质得出∠CDG=∠BCD即可.
∵![]() ,
,![]() (已知),
(已知),
∴EF∥CD_(在同一平面内,垂直于同一条直线的两条直线平行),
∴![]() ∠BCD(两直线平行,同位角相等)
∠BCD(两直线平行,同位角相等)
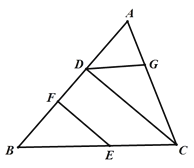
又∵![]() (已知),
(已知),
∴![]() DG(同旁内角互补,两直线平行),
DG(同旁内角互补,两直线平行),
∴![]() ∠BCD(两直线平行,内错角相等)
∠BCD(两直线平行,内错角相等)
∵![]() ∠BCD(已证),
∠BCD(已证),
∴![]() ∠CDG(等量代换).
∠CDG(等量代换).


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】七年级二班的几位同学正在一起讨论一个关于数轴上的点表示数的题目:
甲说:“这条数轴上的两个点![]() 、
、![]() 表示的数都是绝对值是4的数”;
表示的数都是绝对值是4的数”;
乙说:“点![]() 表示负整数,点
表示负整数,点![]() 表示正整数,且这两个数的差是3”;
表示正整数,且这两个数的差是3”;
丙说:“点![]() 表示的数的相反数是它本身”.
表示的数的相反数是它本身”.
(1)请你根据以上三位同学的发言,画出一条数轴,并描出![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个不同的点.
五个不同的点.
(2)求这个五个点表示的数的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
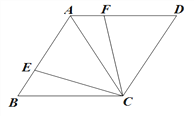
【题目】如图,四边形ABCD中,∠B=60°,对角线AC=BC,点E在AB上,将CE绕点C顺时针旋转60得CF,且点F在AD上.
(1)求证:AF=BE;
(2)若AE=DF,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
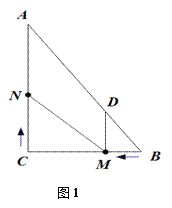
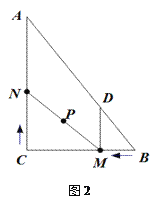
【题目】如图1,在Rt△ABC中,∠C=90,BC=6,AC=8.动点M从点B开始沿边BC向点C以每秒1个单位长度的速度运动,动点N从点C开始沿边CA向点A以每秒2个单位长度的速度运动,点M、N同时出发,且当其中一点到达端点时,另一点也随之停止运动.过点M作MD∥AC,交AB于点D,连接MN.设运动时间为t秒(t≥0).
(1)当t为何值时,四边形ADMN为平行四边形?
(2)是否存在t的值,使四边形ADMN为菱形?若存在,求出t的值;若不存在,说明理由.并探究只改变点N的速度(匀速运动),使四边形ADMN在某一时刻为菱形,求点N的速度;
(3)如图2,在整个运动过程中,求出线段MN中点P所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,EF与AB,CD分别交于点G,H,∠CHG的平分线HM交AB于点M,若∠EGB=50°,则∠GMH的度数为( )
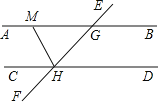
A. 50°B. 55°C. 60°D. 65°
查看答案和解析>>
科目:初中数学 来源: 题型:
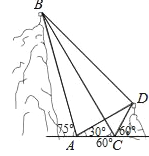
【题目】如图,B,D为两岛上的两座灯塔的塔顶,测量船于水面A处测得B点和D点的仰角分别为75°,30°.于水面C处测得B点和D点的仰角均为60°,AC=0.1km.
(1)试探究图中B,D间距离与另外哪两点间距离相等;
(2)求B点距水平面的高度(计算结果精确到0.01km,参考数据:![]() ≈1.73,tan75°≈3.73)
≈1.73,tan75°≈3.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,A点坐标为(-2,2).
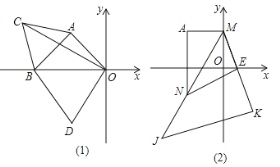
⑴如图⑴,在△ABO为等腰直角三角形,求B点坐标.
⑵如图⑴,在⑴的条件下,分别以AB和OB为边作等边△ABC和等边△OBD,连结OC,求∠COB的度数.
⑶如图⑵,过点A作AM⊥y轴于点M,点E为x轴正半轴上一点,K为ME延长线上一点,以MK为直角边作等腰直角三角形MKJ,∠MKJ=90°,过点A作AN⊥x轴交MJ于点N,连结EN.则①![]() 的值不变;②
的值不变;②![]() 的值不变,其中有且只有一个结论正确,请判断出正确的结论,并加以证明和求出其值.
的值不变,其中有且只有一个结论正确,请判断出正确的结论,并加以证明和求出其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直角三角板![]() 和直角三角板
和直角三角板![]() ,
,![]() ,
,![]() ,
,
![]() .
.
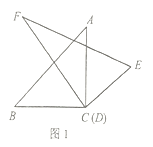
(1)如图1,将顶点![]() 和顶点
和顶点![]() 重合,保持三角板
重合,保持三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 旋转.当
旋转.当![]() 平分
平分![]() 时,求
时,求![]() 的度数;
的度数;
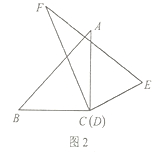
(2)在(1)的条件下,继续旋转三角板![]() ,猜想
,猜想![]() 与
与![]() 有怎样的数量关系?并利用图2所给的情形说明理由;
有怎样的数量关系?并利用图2所给的情形说明理由;
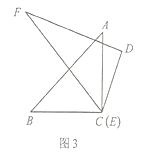
(3)如图3,将顶点![]() 和顶点
和顶点![]() 重合,保持三角板
重合,保持三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 旋转.当
旋转.当![]() 落在
落在![]() 内部时,直接写出
内部时,直接写出![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com