练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

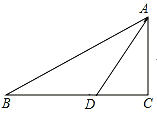
    【题目】已知，如图，∠C＝90°，∠B＝30°，AD是△ABC的角平分线．

    （1）求证：BD＝2CD；

    （2）若CD＝2，求△ABD的面积．

    【答案】（1）见解析；（2）6

    【解析】

    （1）过D作DE⊥AB于E，依据角平分线的性质，即可得到DE=CD，再根据含30°角的直角三角形的性质，即可得出结论；
    （2）依据AD=BD=2CD=4，即可得到Rt△ACD中，，再根据△ABD的面积=进行计算即可．

    解：（1）如图，过D作DE⊥AB于E，


    ∵∠C=90°，AD是△ABC的角平分线，
    ∴DE=CD，
    又∵∠B=30°，
    ∴Rt△BDE中，DE=BD，
    ∴BD=2DE=2CD；

    （2）∵∠C=90°，∠B=30°，AD是△ABC的角平分线，
    ∴∠BAD=∠B=30°，
    ∴AD=BD=2CD=4，
    ∴Rt△ACD中，AC=，

    ∴△ABD的面积为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】若关于的不等式组有三个整数解，且关于的分式方程有整数解，则满足条件的所有整数的和是（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB∥CD，EF与AB，CD分别交于点G，H，∠CHG的平分线HM交AB于点M，若∠EGB＝50°，则∠GMH的度数为（　　）

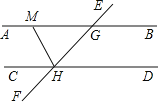
    A. 50°B. 55°C. 60°D. 65°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在平面直角坐标系中，A点坐标为（－2，2）．

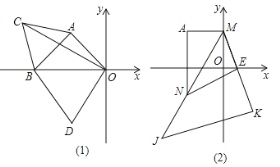
    ⑴如图⑴，在△ABO为等腰直角三角形，求B点坐标．

    ⑵如图⑴，在⑴的条件下，分别以AB和OB为边作等边△ABC和等边△OBD，连结OC，求∠COB的度数．

    ⑶如图⑵，过点A作AM⊥y轴于点M，点E为x轴正半轴上一点，K为ME延长线上一点，以MK为直角边作等腰直角三角形MKJ，∠MKJ=90°，过点A作AN⊥x轴交MJ于点N，连结EN．则①的值不变；②的值不变，其中有且只有一个结论正确，请判断出正确的结论，并加以证明和求出其值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知：∠BAC的平分线与BC的垂直平分线DG相交于点D，DE⊥AB，DF⊥AC，垂足分别为E、F，AB=6，AC=3，则BE=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知直角三角板和直角三角板,,,

    .

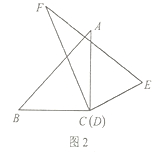
    (1)如图1,将顶点和顶点重合,保持三角板不动,将三角板绕点旋转.当平分时,求的度数；

    (2)在(1)的条件下,继续旋转三角板,猜想与有怎样的数量关系?并利用图2所给的情形说明理由；

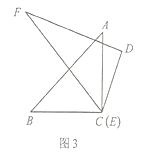
    (3)如图3,将顶点和顶点重合,保持三角板不动,将三角板绕点旋转.当落在内部时,直接写出与的数量关系.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系中，直线y＝﹣x+b与x轴、y轴相交于A、B两点，动点C（m，0）在线段OA上，将线段CB绕着点C顺时针旋转90°得到CD，此时点D恰好落在直线AB上，过点D作DE⊥x轴于点E．

    （1）求m和b的数量关系；

    （2）当m＝1时，如图2，将△BCD沿x轴正方向平移得△B′C′D′，当直线B′C′经过点D时，求点B′的坐标及△BCD平移的距离；

    （3）在（2）的条件下，直线AB上是否存在一点P，以P、C、D为顶点的三角形是等腰直角三角形？若存在，写出满足条件的P点坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】简单多面体是各个面都是多边形组成的几何体，十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）和棱数（E）之间存在一个有趣的关系式，称为欧拉公式．如表是根据左边的多面体模型列出的不完整的表：

    多面体

    顶点数

    面数

    棱数

    四面体

    4

    4

    6

    长方体

    8

    6

    正八面体

    8

    12

    现在有一个多面体，它的每一个面都是三角形，它的面数（F）和棱数（E）的和为30，则这个多面体的顶点数V＝_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）发现：

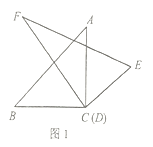
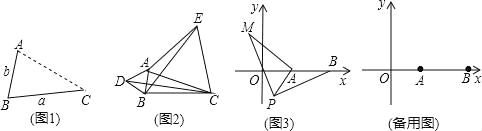
    如图1，点A为线段BC外一动点，且BC=a，AB=b．

    填空：当点A位于　　　 　时，线段AC的长取得最大值，且最大值为　　　 　（用含a，b的式子表示）

    （2）应用：

    点A为线段BC外一动点，且BC=3，AB=1，如图2所示，分别以AB，AC为边，作等边三角形ABD和等边三角形ACE，连接CD，BE．

    ①请找出图中与BE相等的线段，并说明理由；

    ②直接写出线段BE长的最大值．

    （3）拓展：

    如图3，在平面直角坐标系中，点A的坐标为（2，0），点B的坐标为（5，0），点P为线段AB外一动点，且PA=2，PM=PB，∠BPM=90°，请直接写出线段AM长的最大值及此时点P的坐标．

    查看答案和解析>>

    同步练习册答案