
【题目】如图,D 是△ABC 的 BC 边上一点,AB 10,AD 6,DC 2AD,![]() .
.
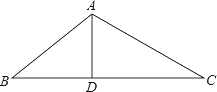
(1)求 AC 的长;
(2)求△ABC 的面积.
【答案】(1)![]() (2)60
(2)60![]()
【解析】
(1)由DC=2AD,根据AD的长求出DC的长,进而求出BD的长,在三角形ABD中,由AB,AD以及BD的长,利用勾股定理的逆定理判断得到三角形为直角三角形,运用勾股定理即可求AC的长.
(2)求BC的长,运用三角形的面积公式即可求出三角形ABC面积.
(1)∵AD=6,DC=2AD,
∴DC=12,
∵![]() ,
,
∴BD=8
在△ABD中,AB=10,AD=6,BD=8,
∵AB2=AD2+BD2,
∴△ABD为直角三角形,即AD⊥BC,
∴AC2= AD2+CD2=180
∴AC=![]()
(2)由(1)得:AD⊥BC
∵BC=BD+DC=8+12=20,AD=6,
∴S△ABC=![]() ×20×6=60.
×20×6=60.


科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块直角三角板ABC(∠A=30°)的斜边AB与一个以r为半径的圆轮子相靠,若BD=1,则r等于( )
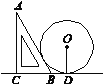
A. 2 B. ![]() C. 1.5 D.
C. 1.5 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
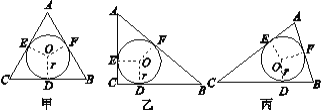
【题目】为了探索三角形的内切圆半径r与三角形的周长C、面积S之间的关系,在数学实验活动中,选取等边三角形图甲和直角三角形图乙进行研究.已知⊙O是△ABC的内切圆,切点分别为D,E,F.
(1)用刻度尺分别量出表中未量度的△ABC的长,填入空格处,并计算出周长C和面积S(结果精确到0.1);
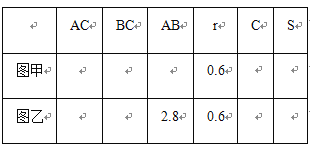
(2)观察图形,利用上表实验数据分析、猜测特殊三角形的r与C,S之间的关系,判断这种关系对任意三角形(图丙)是否也成立,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
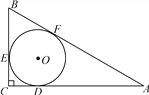
【题目】如图,⊙O为△ABC的内切圆,切点分别为D,E,F,∠C=90°,BC=3,AC=4.
(1)求△ABC的面积;
(2)求⊙O的半径;
(3)求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张正方形纸片,剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去;
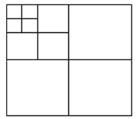
(1)填表
剪的次数 | 1 | 2 | 3 | 4 | 5 |
正方形个数 | 4 | 7 | 10 |
|
|
(2)如果剪n次,共剪出多少个小正方形?
(3)能否经过若干次分割后共得到2019片纸片?若能,请直接写出相应的次数,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电力公司为鼓励市民节约用电,采取按月用电量分段收费办法,已知某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图),根据图象解下列问题:
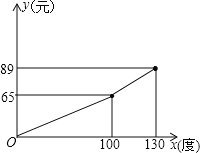
(1)写出y与x的函数关系式;
(2)利用函数关系式,说明电力公司采取的收费标准;
(3)若该用户某月用电60度,则应缴费多少元?若该用户某月缴费105元时,则该用户该月用了多少度电?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com