
【题目】如图,在![]() 中,已知
中,已知![]() ,
,![]() ,
,
(1)画![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 、
、![]() 于点
于点![]() 、
、![]() (保留作图痕迹,作图痕迹请加黑描重);
(保留作图痕迹,作图痕迹请加黑描重);
(2)求![]() 的度数;
的度数;
(3)若![]() ,求
,求![]() 的长度.
的长度.
【答案】(1)见解析;(2)∠A=30°;(3)AD=2cm.
【解析】
(1)如图,利用基本作图作DE垂直平分AB;
(2)利用等腰三角形的性质和三角形内角和计算∠A的度数;
(3)连接BD,如图,根据线段垂直平分线的性质得到DA=DB,则∠ABD=∠A=30°,所以∠CBD=90°,则CD=2BD=2AD,然后利用AC=6cm可计算出AD的长.
解:(1)如图,DE为所作;
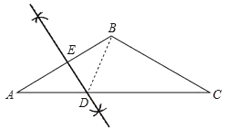
(2)∵AB=BC,
∴∠A=∠C=![]() (180°∠ABC)=
(180°∠ABC)=![]() (180°120°)=30°;
(180°120°)=30°;
(3)连接BD,如图,
∵DE垂直平分AB,
∴DA=DB,
∴∠ABD=∠A=30°,
∴∠CBD=90°,而∠C=30°,
∴CD=2BD,
∴CD=2AD,
∵AC=6cm,即AD+CD=6cm,
∴AD+2AD=6cm,
∴AD=2cm.


科目:初中数学 来源: 题型:
【题目】⑴ 阅读理解
问题1:已知a、b、c、d为正数,![]() ,ac=bd,试说明a=d,b=c.
,ac=bd,试说明a=d,b=c.
我们通过构造几何模型解决代数问题. 注意到条件![]() ,如果把a、b、c、d分别看作为两个直角三角形的直角边,那么可构造图1所示的几何模型.
,如果把a、b、c、d分别看作为两个直角三角形的直角边,那么可构造图1所示的几何模型.
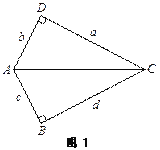
∵ac=bd,
∴AB·CD=BC·AD
∴![]()
请你按照以上思路继续完成说明.
⑵ 深入探究
问题2:若a>0,b>0,试比较![]() 和
和![]() 的大小.
的大小.
为此我们构造图2所示的几何模型,其中AB为直径, O为圆心,点C在半圆上,CD⊥AB 于D,AD=a,BD=b.
请你利用图2所示的几何模型解决提出的问题2.
⑶ 拓展运用
对于函数y=x+![]() ,求当x>0时,求y的取值范围.
,求当x>0时,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(模型建立)
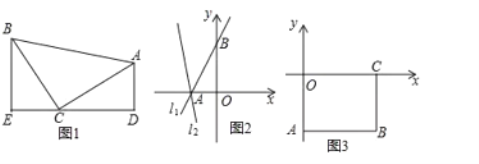
(1)如图1,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() .求证:
.求证:![]() ;
;
(模型应用)
(2)已知直线![]() :
:![]() 与坐标轴交于点
与坐标轴交于点![]() 、
、![]() ,将直线
,将直线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至直线
至直线![]() ,如图2,求直线
,如图2,求直线![]() 的函数表达式;
的函数表达式;
(3)如图3,长方形![]() ,
,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 、
、![]() 分别在坐标轴上,点
分别在坐标轴上,点![]() 是线段
是线段![]() 上的动点,点
上的动点,点![]() 是直线
是直线![]() 上的动点且在第四象限.若
上的动点且在第四象限.若![]() 是以点
是以点![]() 为直角顶点的等腰直角三角形,请直接写出点
为直角顶点的等腰直角三角形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置个平面镜E,使得B,E,D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED).在F处测得旗杆顶A的仰角为39.3°,平面镜E的俯角为45°,FD=1.8米,问旗杆AB的高度约为多少米? (结果保留整数)(参考数据:tan39.3°≈0.82,tan84.3°≈10.02)

查看答案和解析>>
科目:初中数学 来源: 题型:
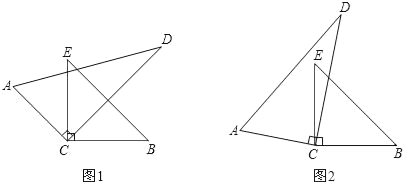
【题目】如图,将一副直角三角形的直角顶点C叠放一起
(1)如图1,若CE恰好是∠ACD的角平分线,请你猜想此时CD是不是的∠ECB的角平分线?并简述理由;
(2)如图1,若∠ECD=α,CD在∠ECB的内部,请猜想∠ACE与∠DCB是否相等?并简述理由;
(3)在如图2的条件下,请问∠ECD与∠ACB的和是多少?并简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F,G,H分别是BD,BC,AC,AD的中点,且AB=CD,下列结论:①EG⊥FH;②四边形EFGH是菱形;③HF平分∠EHG;④EG=![]() (BC﹣AD),其中正确的个数是( )
(BC﹣AD),其中正确的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com